貝爾綱定理
出自 MBA智库百科(https://wiki.mbalib.com/)
貝爾綱定理（Belve's theorem）
目錄 |
貝爾綱定理是指點集拓撲學和泛函分析中的一個重要的工具。這個定理有兩種形式，每一個都給出了拓撲空間是貝爾空間的充分條件。
該定理由勒內-路易•貝爾在他1899年的博士論文中證明。
一個貝爾空間是一個拓撲空間，具有以下性質：對於任意可數個開集Un，它們的交集∩ Un都是稠密的。
（BCT1）每一個完備度量空間都是貝爾空間。更一般地，每一個同胚於某個完備空間的開子集的拓撲空間都是貝爾空間。因此每一個完備可度量化的拓撲空間都是貝爾空間。
（BCT2）每一個局部緊豪斯多夫空間都是貝爾空間。其證明類似於前一個陳述；有限交集性質取得了完備性扮演的角色。
註意從以上任何一個命題都不能推出另一個，因為存在一個不是局部緊的完備度量空間（帶有定義如下的度量的無理數），也存在一個不可度量化空間（不可數福特空間）。
（BCT3）一個非空的完備度量空間不是可數個無處稠密集（也就是閉包具有稠密補集的集合）的並集。
這個表述是BCT1的一個結果，有時更加有用。另外，如果一個非空的完備度量空間是可數個閉集的並集，那麼其中一個閉集具有非空的內部。
以下是完備度量空間X是貝爾空間的一個標準的證明。
設Un為一個開稠密子集的集合。我們希望證明交集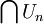
是稠密的。為此，設
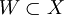為一個開子集。根據稠密性，存在x1和r1 > 0，使得：
。
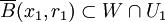遞歸地，我們求出xn和rn > 0，使得：
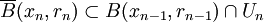而且rn < n − 1。
由於當n > m時，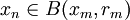
，因此xn是柯西序列，且xn收斂於某個極限x。對於任何n，根據封閉性，有：
。
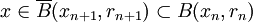因此，對於所有n，都有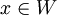
且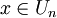
。
BCT1可以用來證明開映像定理、閉圖像定理和一致有界原理。
BCT1也表明每一個沒有孤立點的完備度量空間都是不可數的。（如果X是一個可數的完備度量空間且沒有孤立點，那麼在X中每一個單元素集合都是無處稠密的，因此X在它本身內是第一綱）。特別地，這證明瞭所有實數所組成的集合是不可數的。
BCT1表明以下每一個都是貝爾空間：
·實數空間R；
·無理數，其度量定義為d(x, y) = 1 / (n + 1)，其中n是使x和y的連分數展開式不同的第一個指標（這是一個完備度量空間）；
·康托爾集。
根據BCT2，每一個流形都是貝爾空間，因為它是局部緊空間，也是豪斯多夫空間。這甚至對非仿緊（因此不可度量化）的流形如長直線也是成立的。
