全球专业中文经管百科，由121,994位网友共同编写而成，共计435,837个条目

查看

工具▼

閉圖像定理

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

閉圖像定理（Closed graph theorem）

目錄

1 什麼是閉圖像定理
2 閉圖像定理的證明
3 閉圖像定理的相關推論

什麼是閉圖像定理

　　閉圖像定理是數學中泛函分析的一條定理。

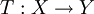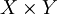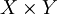　　設 $X$ ， $Y$ 為巴拿赫空間， $T:X \to Y$ 為線性運算元。定義 $T$ 的圖像為 $X \times Y$ 的子空間

　　 $\Gamma (T) = \{(x,T(x))\in X\times Y \vert x \in X\}$ 。

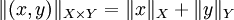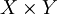　　賦予 $X \times Y$ 範數 $\|(x,y) \|_{X\times Y} = \|x \|_X + \| y \|_Y$ ，使得 $X \times Y$ 成為巴拿赫空間。那麼，這定理指 $T$ 是連續的（與有界等價）當且僅當 $Γ(T)$ 在 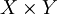$X \times Y$ 內是閉集。

閉圖像定理的證明

　　閉圖像定理可以從開映像定理推導出來。

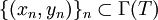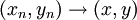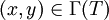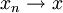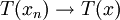　　 $Γ(T)$ 是閉集的充分必要條件是如果序列 $\{(x_n,y_n)\}_n\subset \Gamma(T)$ （即對任意 $n$ 有 $y n = T (x n)$ ），而 $(x_n,y_n) \to (x,y)$ ，那麼 $(x,y)\in \Gamma(T)$ ， $y = T (x)$ 。如果 $T$ 是連續的，從連續性立刻可知 $Γ(T)$ 是閉集，因為連續性是更強的條件：如果 $x_n \to x$ ，則 $T(x_n)\to T(x)$ 。

　　如果 $Γ(T)$ 是閉集，可以在 $Γ(T)$ 定義線性運算元

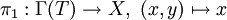　　 $\pi_1: \Gamma (T) \to X,\ (x,y) \mapsto x$ ，

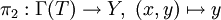　　 $\pi_2: \Gamma (T) \to Y,\ (x,y) \mapsto y$ 。

　　顯然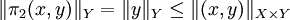 $\|\pi_2(x,y) \|_Y = \|y\|_Y \leq \|(x,y) \|_{X\times Y}$ ，因此 $π 2$ 是有界運算元。

　　 $Γ(T)$ 是巴拿赫空間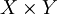 $X\times Y$ 中的閉子空間，所以 $Γ(T)$ 是巴拿赫空間。 $X$ 也是巴拿赫空間， $π 1$ 是雙射，從而由開映射定理的系可知，其逆 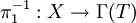$\pi_1^{-1}:X \to \Gamma (T)$ 為有界運算元。

　　因為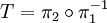 $T = \pi_2 \circ \pi_1^{-1}$ ，故 $T$ 也是有界的。

閉圖像定理的相關推論

　　從這定理可得出黑林格-特普利茨定理──希爾伯特空間上處處定義的對稱線性運算元是有界的。

取自"https://wiki.mbalib.com/zh-tw/%E9%97%AD%E5%9B%BE%E5%83%8F%E5%AE%9A%E7%90%86"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

頁面分類: 數學定理

評論(共0條)

提示:評論內容為網友針對條目"閉圖像定理"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号