詹森不等式
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
詹森不等式（Jensen's inequality），也譯為延森不等式、琴生不等式
目錄 |
[編輯]
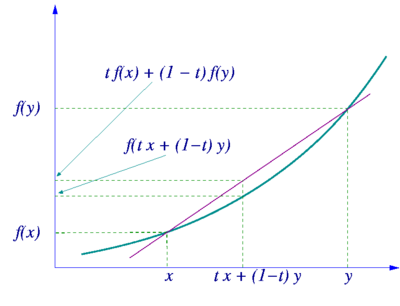
詹森不等式以丹麥數學家約翰·詹森（Johan Jensen）命名。它給出積分的凸函數值和凸函數的積分值間的關係。
[編輯]
詹森不等式可以用測度論或概率論的語言給出。這兩種方式都表明同一個很一般的結果。
[編輯]
假設μ是集合Ω的正測度，使得μ(Ω) = 1。若g是勒貝格可積的實值函數，而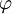
是在g的值域上定義的凸函數，則
。
[編輯]
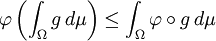以概率論的名詞，μ是個概率測度。函數g換作實值隨機變數X（就純數學而言，兩者沒有分別）。在Ω空間上，任何函數相對於概率測度μ的積分就成了期望值。這不等式就說，若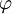是任一凸函數，則
。
[編輯]
[編輯]
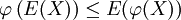假設Ω是實數軸上的可測子集，而f(x)是非負函數，使得
。
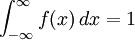以概率論的語言，f是個機率密度函數。
詹森不等式變成以下關於凸積分的命題：
若g是任一實值可測函數，φ在g的值域中是凸函數，則
。
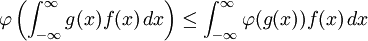若g(x) = x，則這形式的不等式簡化成一個常用特例：
。
[編輯]
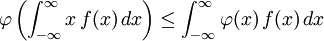若Ω是有限集合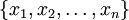
，而μ是Ω上的正規計數測度，則不等式的一般形式可以簡單地用和式表示：
，
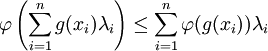其中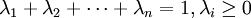
。
若φ是凹函數，只需把不等式符號調轉。
假設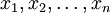
是正實數，g(x) = x，λi = 1 / n及
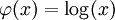。上述和式便成了
，
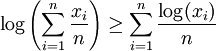兩邊取自然指數就得出熟悉的平均數不等式：
![\frac{x_1 + x_2 + \cdots + x_n}{n} \ge \sqrt[n]{x_1 x_2 \cdots x_n}](/w/images/math/5/9/2/59233828a7dfbc48a6432c0e05a91d32.png)
。
這不等式也有無限項的離散形式。
[編輯]
統計物理學中，若凸函數是指數函數，詹森不等式特別重要：
，
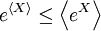其中方括弧表示期望值，是以隨機變數X的某個概率分佈算出。這個情形的證明很簡單（參見Chandler, Sec. 5.5）：在以下等式的第三個指數函數
套用不等式
，
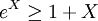即得出所求的不等式。
[編輯]
- Walter Rudin. Real and Complex Analysis. McGraw-Hill. 0-07-054234-1. David Chandler. Introduction to Modern Statistical Mechanics. Oxford. 0-19-504277-8.
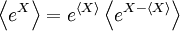
真強！