約翰遜-貝爾曼法則
出自 MBA智库百科(https://wiki.mbalib.com/)
約翰遜-貝爾曼法則(Johnson-Bellman's Rule)
目錄 |
先行工序施工工期短的要排在前面施工後續工序施工工期短的應安排在後面施工。亦即,首先列出m項任務的“工序工期表,然後在表中依次選取最小數,而且每列只選一次,若此數屬於先行工序,則從前排,反之,則從後排。
約翰孫-貝爾曼法則在流水作業中的應用[1]
流水作業法在目前的施工組織設計應用較廣,但在實際應用中常常遇到如何確定施工段合理次序的問題。因為一個施工任務分成若幹個施工段後,每個施工段都要經過相同的若幹道工序。雖然由施工工藝決定的工序順序是不可改變的,但每道工序在各個施工段上的流水順序卻是可以改變的。不同的流水順序總工期不同。這就要求我們要找出一個總工期最短的流水次序。實踐證明,約翰遜——貝爾曼法則能夠較好地解決這個問題。
1.m項任務2道工序,施工次序問題
下麵舉例說明解決此類問題的方法和步驟:例:某工程隊擬對相鄰的五座小橋的基礎工程進行流水作業法施工。經計算隸得各小橋基礎的挖基和砌築基礎兩道工序的工期(日)如表1所示。試確定各小橋基礎的施工次序並確定完成全部任務的總工期。
表1:工序工期表
| 工序 | 橋號 | ||||
| A | B | C | D | E | |
| 挖基 | 4 | 4 | 8 | 6 | 2 |
| 基礎 | 5 | 1 | 4 | 8 | 3 |
第一步,填列“工序工期表”,如表1所示
第二步,繪製“施工次序排列表”的表格,參見表2(熟練以後可不繪此表而在表1中加一欄,直接排序)。
第三步,填表排序。即按約翰遜——貝爾曼法則填充表2,可將各項任務的施工次序排列出來。
表2:施工次序排列
| 填表次序 | 施工次序 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| (1) | - | - | - | - | B |
| (2) | E | - | - | - | - |
| (3) | - | A | - | - | - |
| (4) | - | - | - | C | - |
| (5) | - | - | D | - | - |
| 列中最小數 | 2 | 4 | 6 | 4 | 1 |
| 任務號 | E | A | D | C | B |
在本例中,根據表1,各項任務的施工次序排列如下:
第一個小數為1,在2行2列,屬於後序工序,故填列在表2中施工次序的最後一格,並將表1中B任務這一列划去。
第二個小數為2,在1行5列,屬於先行工序,故填刊在表2中施工次序的最先一格,並將表1中的E任務這一列划去。
餘此類推,將表2填列完畢,可確定各小橋基礎的最優施工次序為:E、A、D、C、B。
第四步,繪製施工進度圖,確定施工總工期。本倒按流水作業法組織施工,其施工進度圖如圖1所示,其總工期為25天。
若不是按約翰遜——貝爾曼法則所確定的施工順序,一般不能取得最短施工總工期。例如本例,若按表1的次序,即按A、B、C、D、E的次序施工,其總工期需要33天。
3.m項任務3道工序時施工次序問題。
對於這類問題,如果符合下列兩種情況中的一種。就有一個簡單的解決辦法。這兩種情況是:
①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即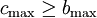 。
。
②第3道工序中的最小施工期Cmax大於或等於第2道工序中的最大施工期bmax。即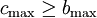 。
。
對於m項任務。3道工序的排序問題,只要符合上述兩條中的一條時。即可按下述方法求得最優施工次序:
第一步。將各項任務中第t道工序和第2道工序的施工期依次加在一起;
第二步,將各項任務中第2道工序和第3道工序的施工期依次加在一起;
第三步,將上兩步中得到的施工工期序列看做2道工序的施工期(參見表3中的a+b,b+c);
第四步,按上述項任務2道工序的方法,求出最優施工次序;
第五步,按所確定的施工次序繪製施工進度圖確定施工總工期。
現舉側說明如下:
例:某工程有5個施工段。3道工序,其各施工段的各工序工期列於表3中。試確定其最優施工次序。
本側按上述方法確定出最憂施工次序為:B、A、E、D、C,總施工期為39無,若按A、B、C、D、E的順序施工,則總工期為42天。
如果m項任務3道工序,不能滿足上述特定條件,就不能用上述簡化方法。通常是採用一種叫樹枝圖的方法。但其計算比較複雜。因此通常對不能滿足特定條件的多藏工段3道工序的施工順序安排。也按3道工序簡化為2道工序的方法作為其近似解。
表3:工序工期表
| 工序 | 施工段 | ||||
| A | B | C | D | E | |
| a | 3 | 2 | 8 | 10 | 5 |
| b | 5 | 2 | 3 | 3 | 4 |
| c | 5 | 6 | 7 | 9 | 7 |
| a+b | 8 | 4 | 11 | 13 | 9 |
| b+c | 10 | 8 | 10 | 12 | 11 |
4.m項任務。工序多於3道時,施工次序的確定
當m>3時。求解最優次序的方法比較複雜。但仍可採用將工序工期按一定方式台並的辦法。分別應用約翰遜——貝爾曼法則,求出相應的總工期,最後再從中選取總工期的最小值,即可確定施工次序的最優安排施工順序的安排,障考慮施工速度快外,同時還要考慮施工費用、施工質量和安全。因此必須從實際出發全面加以考慮,使施工順序的確定能夠為好、快、省並安全地完成施工任務創造條件。
- ↑ 趙輝,張紅雲.約翰遜——貝爾曼法則在流水作業中的應用[J].《河南城建高等專科學校學報》.2001,10(3)
評論(共7條)
①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即cmax\geb_{\max}。 是不是有錯誤?
謝謝指正,錯誤之處已作修改!
①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即cmax\geb_{\max}。 是不是有錯誤?
基礎施工進度圖中第五天到第七天為什麼是空白求指教
想問一下,25是怎麼算出來的?
2+4+6+8+4+1=25,你按EADCB的天數順序列出來,下麵的3584其實都給上面的天數重疊了,所以不用加,而最後一座橋的第二道工序只能單獨做,所以+1.









①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即cmax\geb_{\max}。 是不是有錯誤?