约翰逊-贝尔曼法则
出自 MBA智库百科(https://wiki.mbalib.com/)
约翰逊-贝尔曼法则(Johnson-Bellman's Rule)
目录 |
先行工序施工工期短的要排在前面施工后续工序施工工期短的应安排在后面施工。亦即,首先列出m项任务的“工序工期表,然后在表中依次选取最小数,而且每列只选一次,若此数属于先行工序,则从前排,反之,则从后排。
约翰孙-贝尔曼法则在流水作业中的应用[1]
流水作业法在目前的施工组织设计应用较广,但在实际应用中常常遇到如何确定施工段合理次序的问题。因为一个施工任务分成若干个施工段后,每个施工段都要经过相同的若干道工序。虽然由施工工艺决定的工序顺序是不可改变的,但每道工序在各个施工段上的流水顺序却是可以改变的。不同的流水顺序总工期不同。这就要求我们要找出一个总工期最短的流水次序。实践证明,约翰逊——贝尔曼法则能够较好地解决这个问题。
1.m项任务2道工序,施工次序问题
下面举例说明解决此类问题的方法和步骤:例:某工程队拟对相邻的五座小桥的基础工程进行流水作业法施工。经计算隶得各小桥基础的挖基和砌筑基础两道工序的工期(日)如表1所示。试确定各小桥基础的施工次序并确定完成全部任务的总工期。
表1:工序工期表
| 工序 | 桥号 | ||||
| A | B | C | D | E | |
| 挖基 | 4 | 4 | 8 | 6 | 2 |
| 基础 | 5 | 1 | 4 | 8 | 3 |
第一步,填列“工序工期表”,如表1所示
第二步,绘制“施工次序排列表”的表格,参见表2(熟练以后可不绘此表而在表1中加一栏,直接排序)。
第三步,填表排序。即按约翰逊——贝尔曼法则填充表2,可将各项任务的施工次序排列出来。
表2:施工次序排列
| 填表次序 | 施工次序 | ||||
| 1 | 2 | 3 | 4 | 5 | |
| (1) | - | - | - | - | B |
| (2) | E | - | - | - | - |
| (3) | - | A | - | - | - |
| (4) | - | - | - | C | - |
| (5) | - | - | D | - | - |
| 列中最小数 | 2 | 4 | 6 | 4 | 1 |
| 任务号 | E | A | D | C | B |
在本例中,根据表1,各项任务的施工次序排列如下:
第一个小数为1,在2行2列,属于后序工序,故填列在表2中施工次序的最后一格,并将表1中B任务这一列划去。
第二个小数为2,在1行5列,属于先行工序,故填刊在表2中施工次序的最先一格,并将表1中的E任务这一列划去。
余此类推,将表2填列完毕,可确定各小桥基础的最优施工次序为:E、A、D、C、B。
第四步,绘制施工进度图,确定施工总工期。本倒按流水作业法组织施工,其施工进度图如图1所示,其总工期为25天。
若不是按约翰逊——贝尔曼法则所确定的施工顺序,一般不能取得最短施工总工期。例如本例,若按表1的次序,即按A、B、C、D、E的次序施工,其总工期需要33天。
3.m项任务3道工序时施工次序问题。
对于这类问题,如果符合下列两种情况中的一种。就有一个简单的解决办法。这两种情况是:
①第1道工序中的最小施工期amax大于或等于第2道工序中的最大施工期bmax。即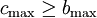 。
。
②第3道工序中的最小施工期Cmax大于或等于第2道工序中的最大施工期bmax。即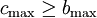 。
。
对于m项任务。3道工序的排序问题,只要符合上述两条中的一条时。即可按下述方法求得最优施工次序:
第一步。将各项任务中第t道工序和第2道工序的施工期依次加在一起;
第二步,将各项任务中第2道工序和第3道工序的施工期依次加在一起;
第三步,将上两步中得到的施工工期序列看做2道工序的施工期(参见表3中的a+b,b+c);
第四步,按上述项任务2道工序的方法,求出最优施工次序;
第五步,按所确定的施工次序绘制施工进度图确定施工总工期。
现举侧说明如下:
例:某工程有5个施工段。3道工序,其各施工段的各工序工期列于表3中。试确定其最优施工次序。
本侧按上述方法确定出最忧施工次序为:B、A、E、D、C,总施工期为39无,若按A、B、C、D、E的顺序施工,则总工期为42天。
如果m项任务3道工序,不能满足上述特定条件,就不能用上述简化方法。通常是采用一种叫树枝图的方法。但其计算比较复杂。因此通常对不能满足特定条件的多藏工段3道工序的施工顺序安排。也按3道工序简化为2道工序的方法作为其近似解。
表3:工序工期表
| 工序 | 施工段 | ||||
| A | B | C | D | E | |
| a | 3 | 2 | 8 | 10 | 5 |
| b | 5 | 2 | 3 | 3 | 4 |
| c | 5 | 6 | 7 | 9 | 7 |
| a+b | 8 | 4 | 11 | 13 | 9 |
| b+c | 10 | 8 | 10 | 12 | 11 |
4.m项任务。工序多于3道时,施工次序的确定
当m>3时。求解最优次序的方法比较复杂。但仍可采用将工序工期按一定方式台并的办法。分别应用约翰逊——贝尔曼法则,求出相应的总工期,最后再从中选取总工期的最小值,即可确定施工次序的最优安排施工顺序的安排,障考虑施工速度快外,同时还要考虑施工费用、施工质量和安全。因此必须从实际出发全面加以考虑,使施工顺序的确定能够为好、快、省并安全地完成施工任务创造条件。
- ↑ 赵辉,张红云.约翰逊——贝尔曼法则在流水作业中的应用[J].《河南城建高等专科学校学报》.2001,10(3)
评论(共7条)
①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即cmax\geb_{\max}。 是不是有錯誤?
谢谢指正,错误之处已作修改!
①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即cmax\geb_{\max}。 是不是有錯誤?
基础施工进度图中第五天到第七天为什么是空白求指教
想问一下,25是怎么算出来的?
2+4+6+8+4+1=25,你按EADCB的天数顺序列出来,下面的3584其实都给上面的天数重叠了,所以不用加,而最后一座桥的第二道工序只能单独做,所以+1.









①第1道工序中的最小施工期amax大於或等於第2道工序中的最大施工期bmax。即cmax\geb_{\max}。 是不是有錯誤?