累計法
出自 MBA智库百科(https://wiki.mbalib.com/)
累計法(Accumulated method)
目錄 |
累計法又稱“方程式法”、“代數平均法”,是指用一個方程式,來表達從最初水平發展,按平均發展速度計算的各期水平的累計總和與相應的各期實際水平的總和一致。
它的基本出發點是:從時間序列的最初發展水平a0開始,以數列的平均速度去代替各期的環比發展速度,由此推算出各期理論發展水平之和與各期實際發展水平之和相一致,即:
解這個高次方程,其正根即為平均發展速度。但是,要求解這個高次方程是非常麻煩的,因此,在實際工作中,往往利用己經編好的《平均增長速度查對錶》來計算。
由此可見,用方程法計算平均發展速度,側重於考察中長期計劃各期水平的總和,亦即計劃期間的累計總量。這種方法適用於計算基本建設投資額、新增固定資產額、住宅建築面積、造林面積等;指標的平均發展速度。
由於建立和解高次方程比較麻煩,因此,在實際工作中都是根據事先編好的《平均增長速度查對錶》,通過查表取得結果。步驟是:
首先,計算各期實際發展水平之和,即各期發展之和除基期發展水平。
其次,判斷是平均增長速度還是平均降低速度,即第一步所得數除以n,若結果大於1,為遞增速度,應查增長速度表,若結果小於1,為遞減速度,應查下降速度表。
最後,根據第一步所得數和n的數值查表,查得平均增(減)速度,如果需要平均發展速度,再按平均發展速度與平均增長速度的關係,將結果轉化為平均發展速度。
例如:某市對“九·五”期間所轄縣國內生產總值進行考評,某縣“九·五”期間(1995—2000年)國內生產總值數據分別為:16565、19262、17740、17723、18944、18160萬元。
某縣“九·五”期間平均發展速度用方程式計算應是第一步所得數596.93%除以5得119.39%,大於100%,表示速度遞增,查表可以知道,這個縣“九·五”期間國內生產總值平均增長速度為6.0%,年平均發展速度為106.0%。
累計法與幾何平均法的比較
用兩種方法求平均發展速度,不論在考察的側重點,還是所應用條件方面均不相同。
幾何平均法的實質是要求從最初水平出發,按所求的平均發展速度發展,計算出的末期水平應等於實際末期水平,這種方法可以只根據最初水平與最末水平計算而不考慮中間水平的變化,其側重點在於考察最末一期發展水平。
累計法的實質是要求從最初水平出發,按所求的平均發展速度計算的各期水平之和,應等於全期實際發展水平的總和。這種方法必須依據全期各期的發展水平才能計算,其側重點在於考察全期發展水平的累計總和。
通過上面的分析可見,選用這兩種方法的哪一種方法求平均發展速度為宜,應視計算對象的特點和不同要求而定。如上述某縣“九·五”期間國內生產總值平均發展速度的計算,本文認為考察的重點為“九·五”期間的全期,因此,用累計法計算較為合理。
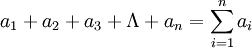
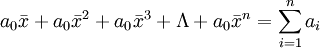
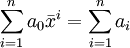
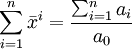








解釋得很好,很受益,謝謝1