矩陣決策法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
1.狀態變數:指可能影響決策後果的各種客觀外界情況或自然狀態.是不可控因素,記為:
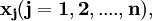 並設
並設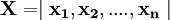 為所有自然狀態的集合。
為所有自然狀態的集合。
2.決策變數:指決策者所採取的各種行動方案,是可控因素。記為: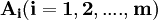 ,並設
,並設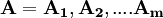 為所有方案的集合。
為所有方案的集合。
3.概率:指各種自然狀態出現的概率。記為: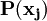 且
且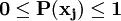 ,
,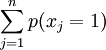
4.損益值:在第j種自然狀態下選取第 種方案所得結果的損益值,記為: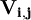 。
。
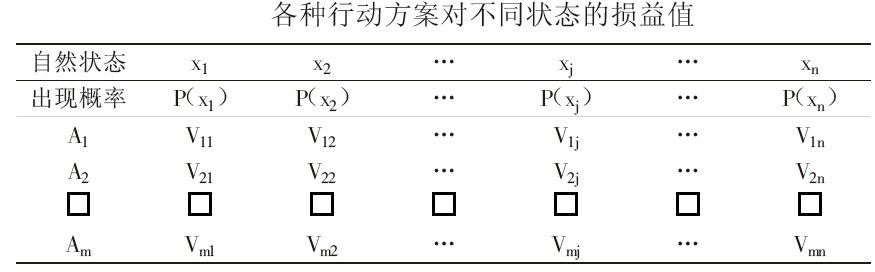
由實際問題給出的條件列出矩陣決策表。一般情況下,是將上述四要素列表如下表:
由表l所給的具體數據,利用期望公式: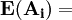
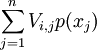
令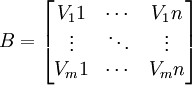 ,
,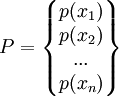 ,
,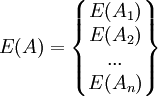 。
。
則有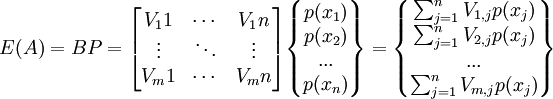
利用最優期望準則公式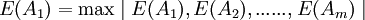 ,確定最優行動方案。
,確定最優行動方案。
當我們利用公式(1)計算出各行動方案的期望值後,加以比較.再由決策目標要求選擇期望值最大(或最小)的行動方案為最優方案。如果表1中的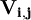 ,是收益值.且決策目標使收益最大,則期望值最大的為最優行動方案;如果
,是收益值.且決策目標使收益最大,則期望值最大的為最優行動方案;如果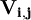 ,決策目標是使損失最小,則選取期望值最小的為最優行動方案。
,決策目標是使損失最小,則選取期望值最小的為最優行動方案。
矩陣決策法的應用舉例[1]
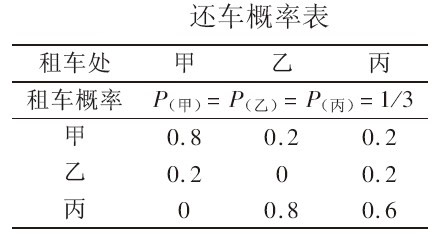
例1:某出租汽車公司在甲、乙、丙三處設立了-租車與還車處,顧客可以在甲、乙、丙任一處租車.也可 在任一處還車。已知顧客在三處租車是等可能的.還車概率如下表所示.如果該公司想選擇一處設立汽車保修廠.間設在何處比較適宜?
解:將還車概率看作設立汽車保修廠的損失值。
令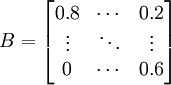 ,
,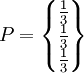 ,
,

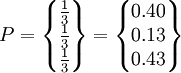
由計算出的期望值看到,經過一定時期的經營後,該公司的每部計程車將被還到甲處的概率為0.40,還到乙處的概率為0.13,還到丙處的概率為0.47。故保修廠應設在丙處為宜。
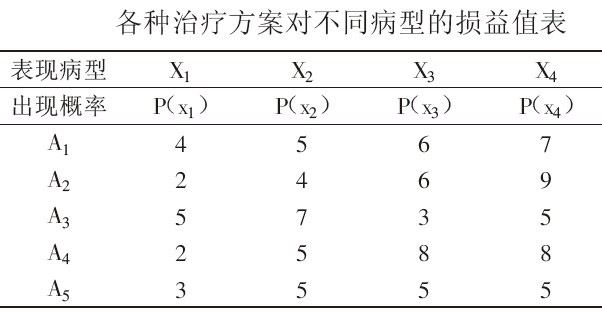
例2:一位病人患某種疾病,該疾病表現的病型為:X1,X2,X3,X4。醫生可以採取下述五種治療方中的一種:放射療法(A1),化學療法(A2),手術療法(A3),藥物療法(A4)和針灸療法(A5)。已知此疾病表現為各種病型的概率p(x_j)及各種治療方案對不同病型的損益值Vij如下表所示。試確定最優治療方案。
解 令 ,
,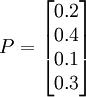 ,則
,則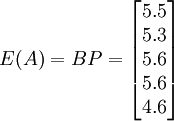
比較計算所得的期望值,手術療法(A3)和藥物療法(A4)都比較好。而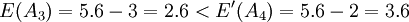 。故最優治療方案為手術療法。
。故最優治療方案為手術療法。
- ↑ 周巨集安.矩陣決策法及其應用.《陝西工學院學報》.2001年1期