亲爱的MBA智库百科用户：

过去的17年，百科频道一直以免费公益的形式为大家提供知识服务，这是我们团队的荣幸和骄傲。然而，在目前越来越严峻的经营挑战下，单纯依靠不断增加广告位来维持网站运营支出，必然会越来越影响您的使用体验，这也与我们的初衷背道而驰。因此，经过审慎地考虑，我们决定推出VIP会员收费制度，以便为您提供更好的服务和更优质的内容。

MBA智库百科VIP会员，您的权益将包括： 1、无广告阅读； 2、免验证复制。

当然，更重要的是长期以来您对百科频道的支持。诚邀您加入MBA智库百科VIP会员，共渡难关，共同见证彼此的成长和进步！

MBA智库百科项目组

2023年8月10日

百科VIP

无广告阅读

免验证复制

1年VIP

¥ 9.9

支付方式：

微信支付

支付宝

PayPal

购买数量：

1

应付金额：

9.9元

汇率换算：

9.9

美元(USD)

按当月汇率换算，

包含手续费

打开手机微信扫一扫继续付款

立即开通

PayPal支付后，可能会遇到VIP权益未及时开通的情况，请您耐心等待，或者联系百科微信客服：mbalib888。

温馨提示：当无法进去支付页面时，可刷新后重试或更换浏览器
开通百科会员即视为同意《MBA智库·百科会员服务规则》

支付成功

全球专业中文经管百科，由121,994位网友共同编写而成，共计436,066个条目

查看

工具▼

相對熵

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

相對熵（Relative Entropy; KL散度; Kullback–Leibler divergence; KLD; 信息散度; 信息增益）

目錄

1 什麼是相對熵
2 相對熵的定義
3 相對熵的特性
4 相對熵和其它量的關係
5 參考文獻

什麼是相對熵

　　相對熵是指兩個概率分佈P和Q差別的非對稱性的度量。相對熵是用來度量使用基於Q的編碼來編碼來自P的樣本平均所需的額外的比特個數。典型情況下，P表示數據的真實分佈，Q表示數據的理論分佈，模型分佈，或P的近似分佈。

相對熵的定義

　　對於離散隨機變數，其概率分佈P 和 Q的相對熵可按下式定義為 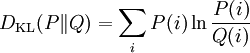$D_{\mathrm{KL}}(P\|Q) = \sum_i P(i) \ln \frac{P(i)}{Q(i)}$ 。即按概率P求得的P和Q的對數差的平均值。相對熵僅當概率P和Q各自總和均為1，且對於任何i皆滿足 $Q (i) > 0$ 及 $P (i) > 0$ 時，才有定義。式中出現 $0ln0$ 的情況，其值按0處理。

　　對於連續隨機變數，其概率分佈P和Q可按積分方式定義為 ^[1]

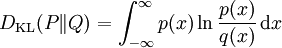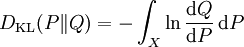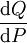　 $D_{\mathrm{KL}}(P\|Q) = \int_{-\infty}^\infty p(x) \ln \frac{p(x)}{q(x)} \, {\rm d}x$ ，其中p和q分別表示分佈P和Q的密度。　　更一般的，若P和Q為集合X的概率測度，且Q關於P絕對連續|絕對連續，則從P到Q的相對熵定義為 $D_{\mathrm{KL}}(P\|Q) = -\int_X \ln \frac{{\rm d}Q}{{\rm d}P} \,{\rm d}P$ ，其中，假定右側的表達形式存在，則 $\frac{{\rm d}Q}{{\rm d}P}$ 為Q關於P的拉東-尼科迪姆定理|R–N導數。

　　相應的，若P關於Q絕對連續|絕對連續，則

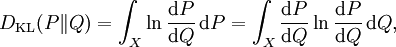
　 $D_{\mathrm{KL}}(P\|Q) = \int_X \ln \frac{{\rm d}P}{{\rm d}Q} \,{\rm d}P = \int_X \frac{{\rm d}P}{{\rm d}Q} \ln\frac{{\rm d}P}{{\rm d}Q}\,{\rm d}Q,$

　　即為P關於Q的相對熵。

相對熵的特性

　　相對熵的值為非負數：

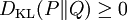　 $D_{\mathrm{KL}}(P\|Q) \geq 0$ ，

　　由吉布斯不等式可知，當且僅當P = Q時D_KL(P||Q)為零。

　　儘管從直覺上相對熵是個度量|度量或距離函數, 但是它實際上並不是一個真正的度量或距離。因為相對熵不具有對稱性：從分佈P到Q的距離（或度量）通常並不等於從Q到P的距離（或度量）。

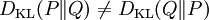
　 $D_{\mathrm{KL}}(P\|Q) \neq D_{\mathrm{KL}}(Q\|P)$

相對熵和其它量的關係

　　自信息和相對熵

　　 $I (m) = D K L (δ i m | p i)$ ,

　　互信息和相對熵

I (X; Y) = D K L (P (X, Y) | | P (X) P (Y)) = E X D K L (P (Y | X) | | P (Y)) = E Y D K L (P (X | Y) | | P (X))

　　信息熵和相對熵

H (X) = E x I (x) = l o g N - D K L (P (X) | | P U (X))

　　條件熵和相對熵

H (X | Y) = l o g N - D K L (P (X, Y) | | P U (X) P (Y)) = (i) l o g N - D K L (P (X, Y) | | P (X)(Y)) - D K L (P (X) | | P U (X)) = H (X) - I (X; Y) = i i l o g N - E Y D K L P (X | Y) | | P U (X)

　　交叉熵和相對熵

　　 $H (p, q) = E p [ - log q] = H (p) + D K L (p | q)$ 。

參考文獻

↑ C. Bishop (2006). Pattern Recognition and Machine Learning. p. 55.

　　

取自"https://wiki.mbalib.com/zh-tw/%E7%9B%B8%E5%AF%B9%E7%86%B5"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目相关课程

金融风险与监管证书（FRR）：资产负债管理体系课程

朱剑文

¥799

金融风险与监管证书（FRR）：市场风险管理体系课程

朱剑文

¥999

探索中国华尔街，抓住未来财富

约翰·s·戈登

¥199

私人银行家，孩子专属的富人思维

李颖

免费

本条目由以下用户参与贡献

頁面分類: 應用數學

評論(共0條)

提示:評論內容為網友針對條目"相對熵"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

以上内容根据网友推荐自动排序生成

官方社群

告MBA智库百科用户的一封信

亲爱的MBA智库百科用户：过去的17年，百科频道一直以免费公益的形式为大家提供知识服务，这是我们团队的荣幸和骄傲。然而，在目前越来越严峻的经营挑战下，单纯依靠不断增加广告位来维持网站运营支出，必然会越来越影响您的使用体验，这也与我们的初衷背道而驰。因此，经过审慎地考虑，我们决定推出VIP会员收费制度，以便为您提供更好的服务和更优质的内容。 MBA智库百科VIP会员（9.9元 / 年，点击开通），您的权益将包括： 1、无广告阅读； 2、免验证复制。当然，更重要的是长期以来您对百科频道的支持。诚邀您加入MBA智库百科VIP会员，共渡难关，共同见证彼此的成长和进步！

MBA智库百科项目组

2023年8月10日

闽公网安备 35020302032707号

添加收藏

新建收藏夹

编辑收藏夹

20

公开（该收藏夹未来有关注者后，将无法设为私密）

私密（仅自己可见）