亲爱的MBA智库百科用户：

过去的17年，百科频道一直以免费公益的形式为大家提供知识服务，这是我们团队的荣幸和骄傲。然而，在目前越来越严峻的经营挑战下，单纯依靠不断增加广告位来维持网站运营支出，必然会越来越影响您的使用体验，这也与我们的初衷背道而驰。因此，经过审慎地考虑，我们决定推出VIP会员收费制度，以便为您提供更好的服务和更优质的内容。

MBA智库百科VIP会员，您的权益将包括： 1、无广告阅读； 2、免验证复制。

当然，更重要的是长期以来您对百科频道的支持。诚邀您加入MBA智库百科VIP会员，共渡难关，共同见证彼此的成长和进步！

MBA智库百科项目组

2023年8月10日

百科VIP

无广告阅读

免验证复制

1年VIP

¥ 9.9

支付方式：

微信支付

支付宝

PayPal

购买数量：

1

应付金额：

9.9元

汇率换算：

9.9

美元(USD)

按当月汇率换算，

包含手续费

打开手机微信扫一扫继续付款

立即开通

PayPal支付后，可能会遇到VIP权益未及时开通的情况，请您耐心等待，或者联系百科微信客服：mbalib888。

温馨提示：当无法进去支付页面时，可刷新后重试或更换浏览器
开通百科会员即视为同意《MBA智库·百科会员服务规则》

支付成功

全球专业中文经管百科，由121,994位网友共同编写而成，共计436,066个条目

查看

工具箱▼

相对熵

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

相对熵（Relative Entropy; KL散度; Kullback–Leibler divergence; KLD; 信息散度; 信息增益）

目录

1 什么是相对熵
2 相对熵的定义
3 相对熵的特性
4 相对熵和其它量的关系
5 参考文献

什么是相对熵

　　相对熵是指两个概率分布P和Q差别的非对称性的度量。相对熵是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的比特个数。典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

相对熵的定义

　　对于离散随机变量，其概率分布P 和 Q的相对熵可按下式定义为 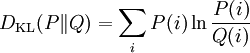$D_{\mathrm{KL}}(P\|Q) = \sum_i P(i) \ln \frac{P(i)}{Q(i)}$ 。即按概率P求得的P和Q的对数差的平均值。相对熵仅当概率P和Q各自总和均为1，且对于任何i皆满足 $Q (i) > 0$ 及 $P (i) > 0$ 时，才有定义。式中出现 $0ln0$ 的情况，其值按0处理。

　　对于连续随机变量，其概率分布P和Q可按积分方式定义为 ^[1]

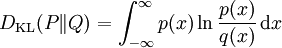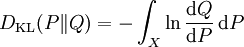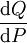　 $D_{\mathrm{KL}}(P\|Q) = \int_{-\infty}^\infty p(x) \ln \frac{p(x)}{q(x)} \, {\rm d}x$ ，其中p和q分别表示分布P和Q的密度。　　更一般的，若P和Q为集合X的概率测度，且Q关于P绝对连续|绝对连续，则从P到Q的相对熵定义为 $D_{\mathrm{KL}}(P\|Q) = -\int_X \ln \frac{{\rm d}Q}{{\rm d}P} \,{\rm d}P$ ，其中，假定右侧的表达形式存在，则 $\frac{{\rm d}Q}{{\rm d}P}$ 为Q关于P的拉东-尼科迪姆定理|R–N导数。

　　相应的，若P关于Q绝对连续|绝对连续，则

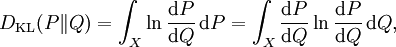
　 $D_{\mathrm{KL}}(P\|Q) = \int_X \ln \frac{{\rm d}P}{{\rm d}Q} \,{\rm d}P = \int_X \frac{{\rm d}P}{{\rm d}Q} \ln\frac{{\rm d}P}{{\rm d}Q}\,{\rm d}Q,$

　　即为P关于Q的相对熵。

相对熵的特性

　　相对熵的值为非负数：

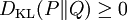　 $D_{\mathrm{KL}}(P\|Q) \geq 0$ ，

　　由吉布斯不等式可知，当且仅当P = Q时D_KL(P||Q)为零。

　　尽管从直觉上相对熵是个度量|度量或距离函数, 但是它实际上并不是一个真正的度量或距离。因为相对熵不具有对称性：从分布P到Q的距离（或度量）通常并不等于从Q到P的距离（或度量）。

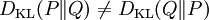
　 $D_{\mathrm{KL}}(P\|Q) \neq D_{\mathrm{KL}}(Q\|P)$

相对熵和其它量的关系

　　自信息和相对熵

　　 $I (m) = D K L (δ i m | p i)$ ,

　　互信息和相对熵

I (X; Y) = D K L (P (X, Y) | | P (X) P (Y)) = E X D K L (P (Y | X) | | P (Y)) = E Y D K L (P (X | Y) | | P (X))

　　信息熵和相对熵

H (X) = E x I (x) = l o g N - D K L (P (X) | | P U (X))

　　条件熵和相对熵

H (X | Y) = l o g N - D K L (P (X, Y) | | P U (X) P (Y)) = (i) l o g N - D K L (P (X, Y) | | P (X)(Y)) - D K L (P (X) | | P U (X)) = H (X) - I (X; Y) = i i l o g N - E Y D K L P (X | Y) | | P U (X)

　　交叉熵和相对熵

　　 $H (p, q) = E p [ - log q] = H (p) + D K L (p | q)$ 。

参考文献

↑ C. Bishop (2006). Pattern Recognition and Machine Learning. p. 55.

　　

来自"https://wiki.mbalib.com/wiki/%E7%9B%B8%E5%AF%B9%E7%86%B5"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目相关课程

超级高效术，让你的人生效率快人10倍

朱丹

¥99 ¥99

腾讯、方太等企业都在学习的商业模式攻略

周永亮博士

¥99

1小时搞懂《行动学习》，助力团队绩效提升

徐佳伟

免费

管理365，10W+经理人都在学的系统管理课

张军博士

¥1588 ¥1588

本条目由以下用户参与贡献

页面分类: 应用数学

评论(共0条)

提示:评论内容为网友针对条目"相对熵"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

以上内容根据网友推荐自动排序生成

官方社群

告MBA智库百科用户的一封信

亲爱的MBA智库百科用户：过去的17年，百科频道一直以免费公益的形式为大家提供知识服务，这是我们团队的荣幸和骄傲。然而，在目前越来越严峻的经营挑战下，单纯依靠不断增加广告位来维持网站运营支出，必然会越来越影响您的使用体验，这也与我们的初衷背道而驰。因此，经过审慎地考虑，我们决定推出VIP会员收费制度，以便为您提供更好的服务和更优质的内容。 MBA智库百科VIP会员（9.9元 / 年，点击开通），您的权益将包括： 1、无广告阅读； 2、免验证复制。当然，更重要的是长期以来您对百科频道的支持。诚邀您加入MBA智库百科VIP会员，共渡难关，共同见证彼此的成长和进步！

MBA智库百科项目组

2023年8月10日

闽公网安备 35020302032707号

添加收藏

新建收藏夹

编辑收藏夹

20

公开（该收藏夹未来有关注者后，将无法设为私密）

私密（仅自己可见）