生日攻擊

出自 MBA智库百科(https://wiki.mbalib.com/)

　　生日攻擊是指在網路安全中利用生日現象，找到衝突的密碼學哈希函數值，偽造報文，攻擊報文身份驗證演算法的模式。

　　一、簽名方案中的生日攻擊

　　艾麗斯要通過某種簽名方案對文檔的散列值簽名來簽署一個電子文檔，假設散列函數產生一個50比特的輸出，她擔心佛瑞德(Fred)哄騙她簽署另外一個合同，也許是關於佛羅里達的沼澤地。由於欺騙性的合同和正確的文檔有相同散列值的概率是1 / 2⁵⁰，這大概是1 / 10¹⁵，因此艾麗斯感覺是安全的。佛瑞德可以嘗試許多欺騙性的合同，但是他找到有相同散列值的合同的可能性非常小，但是佛瑞德研究了生日問題並且照著下麵的方法去做，他找到了能夠對文檔進行細微改變的30個位置：在一行的末尾增加一個空格，略微改變一個詞的拼寫，等等。在每一個位置他有兩個選擇，要麼做一個細微的改變要麼保留原狀，因此他能夠產生2³⁰個本質上與原始文檔相同的文檔，同樣他得到2³⁰個欺騙性的合同並且存儲它們的散列值。考慮最初的生日問題，其中r = 2³⁰並且n = 2⁵⁰，我們有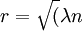).其中λ = 2¹⁰ = 1024。因此一個好文檔的版本和一個欺騙性的合同有相同散列值的概率是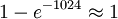。佛瑞德找到這一對匹配的文檔，並且讓艾麗斯簽署其中好的文檔版本，他計劃將她的簽名附加在欺騙性的合同之上，由於它們有相同的散列值，因此簽名對於欺騙性的合同將會有效，所以佛瑞德會聲稱艾麗斯同意購買沼澤地。然而艾麗斯是一個英語教師，她堅持從一個句子中刪除一個逗號，這樣就和佛瑞德要求她簽名的文檔有著完全不同的散列值，佛瑞德又被挫敗了，這時他面臨的問題是找到一個欺騙性的合同和新的正確文檔具有相同的散列值，這根本是不可能的。

　　佛瑞德的行為被稱為生日攻擊，由於生日攻擊有效地將比特數對分，在實際應用中只要你認為有必要，就可以對輸出使用兩次散列函數。對於簽名方案的生日攻擊，艾麗斯所做的是一種可取的方法，在簽名電子文檔時要做一個小的改動。

　　二、基於離散對數的生日攻擊

　　假設我們處理一個大的素數P，並且想要計算L_α(Β)，換句話說，我們想要解α^x = Β(modp)，通過生日攻擊，我們很可能做到。

　　構造兩個列表，長度都大概是；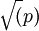

　　1．對於隨機選擇的近似於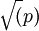的k值，第一個列表包含數字α^k(modp)。

　　2．對於隨機選擇的近似於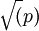的l值，第二個列表包含數字Βα ^{− 1}(modp)。有可能第一個列表的某個元素和第二個列表的某個元素相匹配。如果這樣，我們有

　　α^k = Β ^{− 1}，因此

　　因此，x = k + 1 + l(modp − 1)是期望的離散對數。

　　下麵詳細描述生日攻擊的方法。

　　設h：X->Y是一個Hash函數，X和Y都是有限的，並且|X|>=2|Y|，記|X|=m，|Y|=n。顯然至少有n個碰撞，問題是如何去找到這些碰撞。一個很自然的方法是隨機選擇k個不同的元素x1,x2,x3,.....,xk ∈X,計算yI=h(xi)，1<=i<=k，然後確定是否有一個碰撞發生。這個過程類似於把k個球隨機地扔到n個箱子裡邊，然後檢查看是否某一箱子裡邊至少有兩個球。k個球對應於k個隨機數x1,x2,x3,.....,xk，n個箱子對應於Y中的n個可能的元素。我們將計算用這種方法找到一個碰撞的概率的下界，該下界只依賴於k和n，而不依賴於m。

　　因為我們關心的是碰撞概率的下界，所以可以假定對所有y∈Y，有|h-1(y)|≈m/n。這個假定是合理的，這是因為如果原像集h-1(y)( y∈Y)不是近似相等的，那麼找到一個碰撞的概率將增大。

　　因為原像集h-1(y)( y∈Y)的個數都近似相等，並且xI(1<=i<=k)是隨機選擇的，所以可將yI=h(xi)，1<=i<=k視作Y中的隨機元素（yi(1<=i<=k)未必不同）。但計算k個隨機元素y1,y2, .....yk∈Y是不同的概率是一件容易的事情。依次考慮y1,y2, .....yk。y1可任意地選擇；y2 ≠y1的概率為1-1/n；y3 ≠y1 ,y2的概率為1-2/n；.....；yk ≠y1,y2, .....,yk-1的概率為1-(k-1)/n。

　　因此，沒有碰撞的概率是（1-1/n）(1-2/n）.....(1-(k-1)/n）。如果x是一個比較小的實數，那麼1-x≈e-x，這個估計可由下式推出：e-x=1-x+x2/2!-x3/3!+ .....。現在估計沒有碰撞的概率（1-1/n）(1-2/n）.....(1-(k-1)/n）約為1-e-k(k-1)/2n。我們設ε是至少有一個碰撞的概率，則ε≈1-e-k(k-1)/2n，從而有k2-k≈nln(1/(1-ε)2)。去掉-k這一項，我們有k2≈nln(1/(1-ε)2)，即k≈sqrt(2nln(1/(1-ε)2))。

　　如果我們取ε=0.5，那麼k≈1.17 sqrt(n)。這表明，僅sqrt(n)個X的隨機的元素就能以50%的概率產生一個碰撞。註意ε的不同選擇將導致一個不同的常數因數，但k與sqrt(n)仍成正比例。

　　如果X是一個教室中的所有學生的集合，Y是一個非閏年的365天的集合，h(x)表示學生x的生日，這時n=365，ε=0.5，由k≈1.17 sqrt(n)可知，k≈22.3。因此，此生日問題的答案為23。

　　生日攻擊隱含著消息摘要的長度的一個下界。一個40比特長的消息摘要是很不安全的，因為僅僅用220（大約一百萬）次隨機Hash可至少以1/2的概率找到一個碰撞。為了抵抗生日攻擊，通常建議消息摘要的長度至少應取為128比特，此時生日攻擊需要約264次Hash。安全的Hash標準的輸出長度選為160比特是出於這種考慮。

　　中間相遇攻擊是生日攻擊的一種變形，它不比較Hash值，而是比較鏈中的中間變數。這種攻擊主要適用於攻擊具有分組鏈結構的Hash方案。中間相遇攻擊的基本原理為：將消息分成兩部分，對偽造消息的第一部分從初試值開始逐步向中間階段產生r1個變數；對偽造消息的第二部分從Hash結果開始逐步退回中間階段產生r2個變數。在中間階段有一個匹配的概率與生日攻擊成功的概率一樣。

　　在修正分組攻擊中，為了修正Hash結果並獲得期望的值，偽造消息和一個分組級聯。這種攻擊通常應用於最後一個組，因此也稱為修正最後分組攻擊。差分分析是攻擊分組密碼的一種方法。這種攻擊也可用來攻擊某些Hash演算法。

　　針對Hash演算法的一些弱點可對Hash演算法進行攻擊，可利用Hash演算法的代數結構及其所使用的分組密碼的弱點來攻擊一些Hash方案。例如針對DES的一些弱點（即互補性、弱密鑰、密鑰碰撞等）來攻擊基於DES的Hash方案。

• 生日悖論