生日悖論
出自 MBA智库百科(https://wiki.mbalib.com/)
生日悖論(Birthday paradox)
目錄 |
生日悖論(Birthday paradox)是指,如果一個房間里有23個或23個以上的人,那麼至少有兩個人的生日相同的概率要大於50%。這就意味著在一個典型的標準小學班級(30人)中,存在兩人生日相同的可能性更高。對於60或者更多的人,這種概率要大於99%。從引起邏輯矛盾的角度來說生日悖論並不是一種悖論,從這個數學事實與一般直覺相抵觸的意義上,它才稱得上是一個悖論。大多數人會認為,23人中有2人生日相同的概率應該遠遠小於50%。計算與此相關的概率被稱為生日問題,在這個問題之後的數學理論已被用於設計著名的密碼攻擊方法:生日攻擊。
理解生日悖論的關鍵在於領會相同生日的搭配可以是相當多的。如在前面所提到的例子,23個人可以產生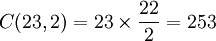 種不同的搭配,而這每一種搭配都有成功相等的可能。從這樣的角度看,在253種搭配中產生一對成功的配對也並不是那樣的不可思議。
種不同的搭配,而這每一種搭配都有成功相等的可能。從這樣的角度看,在253種搭配中產生一對成功的配對也並不是那樣的不可思議。
換一個角度,如果你進入了一個有著22個人的房間,房間里的人中會和你有相同生日的概率便不是50:50了,而是變得非常低。原因是這時候只能產生22種不同的搭配。生日問題實際上是在問任何23個人中會有兩人生日相同的概率是多少。
假設有n個人在同一房間內,如果要計算有兩個人在同一日出生的機率,在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。
電腦率的方法是,首先找出p(n)表示n個人中,每個人的生日日期都不同的概率。假如n > 365,根據鴿巢原理其概率為0,假設n ≤ 365,則概率為:
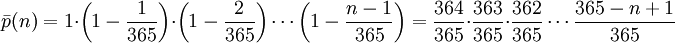
因為第二個人不能跟第一個人有相同的生日(概率是364/365),第三個人不能跟前兩個人生日相同(概率為363/365),依此類推。用階乘可以寫成如下形式:
p(n)表示n個人中至少2人生日相同的概率:

n≤365,根據鴿巢原理, n大於365時概率為1。
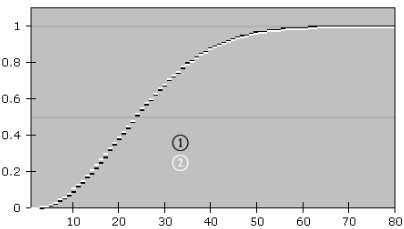
當n=23發生的概率大約是0.507。其他數字的概率用上面的演算法可以近似的得出來:
| n | p(n) |
|---|---|
| 10 | 12% |
| 20 | 41% |
| 30 | 70% |
| 50 | 97% |
| 100 | 99.99996% |
| 200 | 99.9999999999999999999999999998% |
| 300 | 1 − (7 × 10−73) |
| 350 | 1 − (3 × 10−131) |
| ≥366 | 100% |
註意所有人都是隨機選出的:作為對比,q(n)表示房間中 n個其他人中與特定人(比如你)有相同生日的概率:
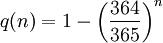
當n = 22時概率只有大約0.059,約高於十七分之一。如果n個人中有50%概率存在某人跟你有相同生日, n至少要達到253 。註意這個數字大大高於 .究其原因是因為房間內可能有些人生日相同。==數學論證(非數字方法)==
.究其原因是因為房間內可能有些人生日相同。==數學論證(非數字方法)==
在 Paul Halmos 的自傳中,他認為生日悖論僅通過數值上的計算來解釋是一種悲哀。為此,Paul Halmos給出了一種概念數學方法的解釋,下麵就是這種方法(儘管這個方法包含一定的誤差)。
乘積: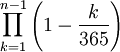
等於 1-p(n), 因此我們關註第一個n,使得乘積小於1/2,這樣我們得到:
![\sqrt[n-1]{\prod_{k=1}^{n-1}\left(1k \over 365}\right)}<{1 \over n-1}\sum_{k=1}^{n-1}\left(1k \over 365}\right)](/w/images/math/3/b/2/3b292143b2a05a91f95e6e2ad86d5769.png)
由平均數不等式得:
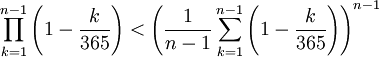
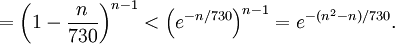
(我們首先利用已知的1到n-1所有整數和等於 n(n-1)/2, 然後利用不等式不等式 1-x < e−x.)
如果僅當:
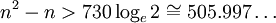
最後一個表達式的值會小於0.5。
其中"loge"表示自然對數。這個數略微小於506,運氣稍微好一點點就可以達到506,等於n2-n,我們就得到n=23。
在推導中,Halmos寫道:
這個推導是基於一些數學系學生必須掌握的重要工具。生日問題曾經是一個絕妙的例子,用來演示純思維是如何勝過機械計算:一兩分鐘就可以寫出這些不等式,而乘法運算則需要更多時間,並更易出錯,無論使用的工具是一隻鉛筆還是一臺老式電腦。計算器不能提供的是理解力,或數學才能,或產生更高級、普適化理論的堅實基礎。[1]。
然而Halmos的推導只顯示至少需要23人保證平等機會下的生日匹配;因為我們不知道給出的不等式有多清晰,因此n=22能夠正切的可能也無法確定。
生日悖論可以推廣一下:假設有n 個,每一個人都隨機地從1和特定的N個數中選擇出來一個數(N可能是365或者其他的大於0的整數)。
p(n)表示有兩個人選擇了同樣的數字,這個概率有多大?
下麵的逼近公式可以回答這個問題
下麵我們泛化生日問題: 給定從符合離散均勻分佈的區間[1,d]隨機取出n個整數, 至少2個數字相同的概率p(n;d) 有多大?
類似的結果可以根據上面的推導得出。
反算問題可能是:
- 對於確定的概率 p ...
- ... 找出最大的 n(p)滿足所有的概率p(n)都小於給出的p,或者
- ... 找出最小的n(p) 滿足所有的概率p(n)都大於給定的p。
對這個問題有如下逼近公式:
| 逼近 | 估計N :=365 | |||||
| p | n 推廣 | n <N :=365 | n↓ | p(n↓) | n↑ | p(n↑) |
0.01 | 0.14178 √N | 2.70864 | 2 | 0.00274 | 3 | 0.00820 |
| 0.05 | 0.32029 √N | 6.11916 | 6 | 0.04046 | 7 | 0.05624 |
0.1 | 0.45904 √N | 8.77002 | 8 | 0.07434 | 9 | 0.09462 |
0.2 | 0.66805 √N | 12.76302 | 12 | 0.16702 | 13 | 0.19441 |
| 0.3 | 0.84460 √N | 16.13607 | 16 | 0.28360 | 17 | 0.31501 |
| 0.5 | 1.17741 √N | 22.49439 | 22 | 0.47570 | 23 | 0.50730 |
| 0.7 | 1.55176 √N | 29.64625 | 29 | 0.68097 | 30 | 0.70632 |
| 0.8 | 1.79412 √N | 34.27666 | 34 | 0.79532 | 35 | 0.81438 |
| 0.9 | 2.14597 √N | 40.99862 | 40 | 0.89123 | 41 | 0.90315 |
| 0.95 | 2.44775 √N | 46.76414 | 46 | 0.94825 | 47 | 0.95477 |
0.99 | 3.03485 √N | 57.98081 | 57 | 0.99012 | 58 | 0.99166 |
註意:某些值被著色,說明逼近不總是正確。
生日悖論可以用電腦代碼經驗性模擬
days := 365;
numPeople := 1;
prob := 0.0;
while prob < 0.5 begin
numPeople := numPeople + 1;
prob := 1 - ((1-prob) * (days-(numPeople-1)) / days);
print "Number of people: " + numPeople;
print "Prob. of same birthday: " + prob;
end;
生日悖論普遍的應用於檢測哈希函數:N-位長度的哈希表可能發生碰撞測試次數不是2N次而是只有2N/2次。這一結論被應用到破解密碼學散列函數的生日攻擊中。
生日問題所隱含的理論已經在(Schnabel 1938)名字叫做capture-recapture的統計試驗得到應用,來估計湖裡魚的數量。
此問題另外一個範化就是求得要在隨機選取多少人中才能找到2個人生日相同,相差1天,2天等的概率大於50% 。這是個更難的問題需要用到容斥原理。結果(假設生日依然按照平均分佈)正像在標準生日問題中那樣令人吃驚:
| 2人生日相差k天 | #需要的人數 |
|---|---|
| 0 | 23 |
| 1 | 14 |
| 2 | 11 |
| 3 | 9 |
| 4 | 8 |
| 5 | 7 |
| 7 | 6 |
只需要隨機抽取6個人,找到兩個人生日相差一周以內的概率就會超過50%。
- ↑ 原文:The reasoning is based on important tools that all students of mathematics should have ready access to. The birthday problem used to be a splendid illustration of the advantages of pure thought over mechanical manipulation; the inequalities can be obtained in a minute or two, whereas the multiplications would take much longer, and be much more subject to error, whether the instrument is a pencil or an old-fashioned desk computer. What calculators do not yield is understanding, or mathematical facility, or a solid basis for more advanced, generalized theories
2.Zoe Emily Schnabel: "The estimation of the total fish population of a lake"(某湖中魚類總量估計), 美國數學月刊 45 (1938年), 348-352頁
3.M. Klamkin,D. Newman: "Extensions of the birthday surprise"(生日驚喜的擴充), Journal of Combinatorial Theory 3 (1967年),279-282頁。
4.D. Blom: "a birthday problem"生日問題, 美國數學月刊 80 (1973年),1141-1142頁。{這一論文證明瞭當生日按照平均分佈,兩個生日相同的概率最小。)
評論(共58條)
100:99.99996%;200:99.9999999999999999999999999998%;那麼200-100=100人中所起到的作用是多少
還是覺得不太可能,如果隨機抽取25人的話,如果他們其中真的沒有人是同一天生日的了? 又該怎麼解釋 這種解釋只能存在在某一條件下~~
還是覺得不太可能,如果隨機抽取25人的話,如果他們其中真的沒有人是同一天生日的了? 又該怎麼解釋 這種解釋只能存在在某一條件下~~
25人上述也只說了可能性在百分之五十以上啊,一半的可能嘛,就算沒有也是正常的啊,只是那種情況概率大些的問題
那麼60億人裡面幾乎有1.2億人生日相同!!!!
不是這樣理解的~ 這是說60億人裡面 100%有兩個人生日相同 因為只要n>365就保證100%
那麼60億人裡面幾乎有1.2億人生日相同!!!!
你邏輯不行
那麼60億人裡面幾乎有1.2億人生日相同!!!!
不可能吧!那麼60/1.2=50,那不是只有那50天有人出生嗎?其它300多天干嘛去了呢
不可能吧!那麼60/1.2=50,那不是只有那50天有人出生嗎?其它300多天干嘛去了呢
生日的話,N < 365.
如果班上有30人,我和某個人生日同一天的概率是30/365。如果有兩個人的生日是同一天,概率是30*29*(30/365)
你邏輯不行
有多少人生日相同,哪能這麼算啊,算下每天出生多少人不就得了。
還是覺得不太可能,如果隨機抽取25人的話,如果他們其中真的沒有人是同一天生日的了? 又該怎麼解釋 這種解釋只能存在在某一條件下~~
什麼叫概率,同學。 概率表達的東西,本來就存成不確定性。
不可能的,要是有366個人的話,肯定有兩個人的生日相同
那麼60億人裡面幾乎有1.2億人生日相同!!!!
看來你完全沒看懂呀,建議你再看一遍
什麼叫概率,同學。 概率表達的東西,本來就存成不確定性。
對的,先搞清楚概率的含義,如果你抽取25人的話,25人的生日已經是定數,所謂的概率已經被你限制。
不可能的,要是有366個人的話,肯定有兩個人的生日相同
他想說的是潤年。。。2月29號
那麼60億人裡面幾乎有1.2億人生日相同!!!!
好好學學數學吧
.後悔當初上學的時候,沒問有沒有跟我相同生日的... 班上五十多人,這個概率無窮逼近100%了...
兄弟你沒看懂
不可能的,要是有366個人的話,肯定有兩個人的生日相同
閏年。極端情況1x2x3...x365...
.後悔當初上學的時候,沒問有沒有跟我相同生日的... 班上五十多人,這個概率無窮逼近100%了...
這個理解是錯的,五十多個人中,出現“兩個生日相同的人”的可能性和“出現和某個特定人生日相同”的可能性是不等價的。你說的這個概率大概在 50/365
那麼60億人裡面幾乎有1.2億人生日相同!!!!
。。。。。。。。。。。。。。你這問題跟上面的問題不一樣了。 你這問題的答案是60億除以365.25了。
那麼60億人裡面幾乎有1.2億人生日相同!!!!
...你數學老師肯定很無奈
how come?
怎麼會這樣呢? 總覺得不可能會那麼地巧合! 你想想…… 100個人中有兩個人生日相同的概率是999996% 那幾乎是1
在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。
怎麼會這樣呢? 總覺得不可能會那麼地巧合! 你想想…… 100個人中有兩個人生日相同的概率是999996% 那幾乎是1
在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。
怎麼會這樣呢? 總覺得不可能會那麼地巧合! 你想想…… 100個人中有兩個人生日相同的概率是999996% 那幾乎是1
你要反著想,你要在100個人裡面,100個都不同生日,那個機率幾乎是0.....
還是覺得不太可能,如果隨機抽取25人的話,如果他們其中真的沒有人是同一天生日的了? 又該怎麼解釋 這種解釋只能存在在某一條件下~~
隨機,前提是隨機
還是覺得不太可能,如果隨機抽取25人的話,如果他們其中真的沒有人是同一天生日的了? 又該怎麼解釋 這種解釋只能存在在某一條件下~~
25個人概率是大於50%但不是同一天生日也是可能(可以存在)的
還是覺得不太可能,如果隨機抽取25人的話,如果他們其中真的沒有人是同一天生日的了? 又該怎麼解釋 這種解釋只能存在在某一條件下~~
概率是50%啊..
不可能的,要是有366個人的話,肯定有兩個人的生日相同
閏年有366天,有可能366人生日都不一樣
100:99.99996%;200:99.9999999999999999999999999998%;那麼200-100=100人中所起到的作用是多少
提升概律姓
不可能吧!那麼60/1.2=50,那不是只有那50天有人出生嗎?其它300多天干嘛去了呢
可能與女人的生理期有關吧,能懷孕的機會不一樣?
不可能吧!那麼60/1.2=50,那不是只有那50天有人出生嗎?其它300多天干嘛去了呢
他是人才 你是天才
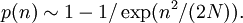


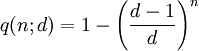

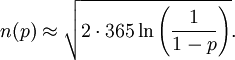








怎麼會這樣呢? 總覺得不可能會那麼地巧合! 你想想…… 100個人中有兩個人生日相同的概率是999996% 那幾乎是1