鴿巢原理

出自 MBA智库百科(https://wiki.mbalib.com/)

鴿巢原理(Pigeonhole Principle)

　　鴿巢原理又名抽屜原理或狄利克雷原理，它由德國數學家狄利克雷(Divichlet，1805—1855)首先發現。鴿巢原理在組合學中占據著非常重要的地位，它常被用來證明一些關於存在性的數學問題，並且在數論和密碼學中也有著廣泛的應用。使用鴿巢原理解題的關鍵是巧妙構造鴿巢或抽屜，即如何找出合乎問題條件的分類原則。^[1]

　　鴿巢原理的簡單形式：如果n+1個物體被放進n個盒子，那麼至少有一個盒子包含兩個或者更多的物體。

　　證明：如果這n個盒子中的每一個都至多含有一個物體，那麼物體的總數最多是n。既然我們有n+1個物體，於是某個盒子就必然包含至少兩個物體。

　　鴿巢原理的加強形式：令Q₁，Q₂，……，Q_n為正整數，如果將Q₁+Q₂+…+Q_n-n+1個物體放入n個盒子內，那麼，或者第一個盒子至少含有Q₁個物體，或者第二個盒子至少含有Q2個物體，……，或者第n個盒子至少含有Q_n個物體。

　　證明：設將Q₁+Q₂+…+Q_n-n+1個物體分放到n個盒子中，如果對於每個i=1，2，…，n，第i個盒子含有少於Q_i個物體，那麼所有盒子中的物體總數不超過(Q₁-1)+(Q₂-1)+…+(Q_n-1)=Q₁+Q₂+…+Q_n-n，該數比所分發的物體總數少1，所以我們斷定，對於某一個i=1，2，…，n，第i個盒子至少包含Q_i個物體。

　　由上面的原理可得如下推論：推論1：m雙鞋放入n個鞋盒中，則至少有一個盒子中有不少於[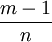]雙鞋。

　　推論2：n(m-1)+1只鴿子放入n個鴿籠，則至少有一個鴿籠中有m只鴿子。

　　推論3：設m₁，m₂，…，m_n均為正整數，且滿足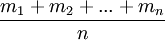>r-1，則m₁，m₂，…，m_n申至少有一個數不小於r。

　　1.用於幾何圖形

　　(1)在邊長為1的等邊三角形內任意選擇5個點，存在2個點，其間距離至多為1/2。

　　證明：由題意，可以構造出4個抽屜，每個抽屜滿足在其問的距離至多為1/2(見圖1)。根據鴿巢原理，在4個抽屜里分別放置4個點，不論第5個點如何放置，都滿足兩點之間的距離最多為1/2。

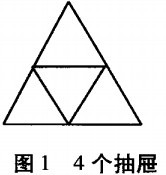
　　(2)證明在邊長為1的等邊三角形內任意選擇10個點，存在兩個點，其間距離至多為1/3。

　　證明：按照圖2的構造可以證明該題。

　　歸納：在邊長為1的等邊三角形內任意選擇n²+1個點，存在2個點，其間距離為。

　　(3)在單位正方形內任意給定51個點，求證至少有三個點落在一個半徑為1/7的圓內。

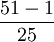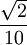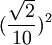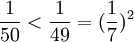　　證明：將單位正方形的各邊五等分，以此把它分成25個邊長為l/5的小正方形，作為25個抽屜。根據抽屜原理可知，其中至少有一個小正方形中含有[]+1=3個點，而這樣的小正方形外接圓半徑是。又由得得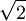/10<1/7，所以至少有三個點在半徑為1/7的一個圓內。

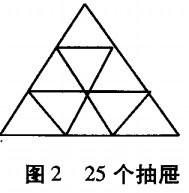
　　(4)在直徑為5的圓內任意給定10個點，證明存在兩個點，它們之間的距離小於2。

　　證明：根據題意，我們最先考慮到把圓等分成9個扇形而構造出9個抽屜，但是雖然必有兩個點在某一扇形內，但不能確認它們之間的距離小於2。於是我們考慮先用一個與已知圓同心，半徑為1的不包含邊界的小圓作為一個抽屜，然後再把圓環部分等分成八個部分，(如圖3所示)這樣就構成了9個抽屜。

　　根據抽屜原理可知，存在兩個點在同一個抽屜(包括邊界)中，若這兩個點在小圓(不包含邊界)中，顯然它們之間的距離小於2。若這兩個點在圓環部分的八個等分中的某一圖形里，不妨設在圖形ABCD中。由於

　　由此可知，這時兩個點之間的距離也小於2，從而命題得證。

　　2.用於數的整除關係

　　(1)在前12個自然數中任取7個數，一定存在兩個數，其中的一個數是另一個數的整數倍。

　　分析：若能把前12個自然數劃分成6個集合，即構成6個抽屜，使每個抽屜內的數或只有一個，或有任意的兩個數，其中的一個是另一個的整數倍，這樣就可以由抽屜原理推出結論。那麼如何對這12個自然數進行分組?我們知道，一個自然數，它要麼是奇數，要麼是偶數。若是偶數，我們總能把它表達為奇數與2^k(K=1，2，3，…)的乘積的形式。這樣，如果允許上述乘積中的因數2^k的指數K可以等於零，則每一個自然數都可表達成“奇數×2^k(K=0，1，2，…)的形式，於是，把這12個自然數用上述表達式進行表達，並把式中“奇數”部分相同的自然數作為一組，構成一個抽屜。

　　證明：把前12個自然數劃分為如下六個抽屜：

　　A₁={l·2⁰，l·2¹，l·2²，1·2³}

　　A₂={3·2⁰，3·2¹，3·2²}

　　A₃={5·2⁰，5·2¹}

　　A₄={7·2⁰}

　　A₅={9·2⁰}

　　A₆={11·2⁰}

　　顯然，上述六個抽屜內的任意兩個抽屜無公共元素，且A₁+A₂+A₃+A₄+A₅+A₆={1，2，3，…，12}。由鴿巢原理，對於前12個自然數不論以何種方式從其中取出7個數，必定存在兩個數同在A₁或A₂或A₃抽屜里，那麼這兩個數之間存在倍數關係。即一個數是另一個數的整數倍。

　　歸納：從1到2n的正整數中任取n+1個數，則這n+1個數中至少有兩個數，其中一個數是另一個數的倍數。

　　證明：設這n+1個數為a_l，a₂，…，a_n，a_{n + 1}，我們對其中的每一個數都進行如下的處理：去掉一切2的因數，直到剩下奇數為止。例如，20=2²×5，去掉2留下奇數5，結果可得到n+1個奇數r₁，r₂，…，r_n，r_{n + l}。顯然1≤r₁，r₂，…，r_n，r_{n + l}<2_n，而1到2n中只有n個奇數，由抽屜原理知，上面n+1個奇數中至少有兩個數是相同的，設這兩個數為r_i=r_j(i≠j)，它們分別代表的整數為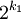×r_i和×r_j,不論它們誰大誰小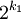，和也之間總存在倍數關係，即一個數是另一個數的整數倍。

　　(2)證明任意五個整數中，必有三個整數的和是3的倍數。

　　證明：任一整數被3除餘數只可能是0，l，2。

　　若給定的五個整數被3除所得的餘數中0，l，2都出現，那麼餘數分別為O，l，2的三個數的和一定能被3整除，如果餘數中至多只出現0，l，2中的兩個，那麼由抽屜原理，其中必有一個餘數至少出現三次。而這餘數相同的三個數的和一定能被3整除。

　　(3)證明對任意給定的52個整數，存在其中的兩個整數，要麼兩者的和能被100整除，要麼兩者的差能被100整除。

　　證明：任意一個整數a除以100產生的餘數不外乎為O，1，2，…，99。題目中的52個整數a_i除以100則產生52個餘數r_i(i=1，2，…，52)。

　　如果這52個餘數中有兩個餘數相等，即r_i=r_j(i≠j)，那麼一定有a_i-a_j能被100整除。即存在兩個數，它們的差能被100整除。

　　如果這52個餘數均不相等，我們現在對0，1，2，…，99這100個數來構造抽屜，將相加之和為100的兩個數放在同一個抽屜里。

　　構造出來的51個抽屜如下：{1，99}，{2，98}，{3，97},...，{49，51}，{0}，{50}由於有52個不同的餘數，根據鴿巢原理，必有兩個餘數來自同一個抽屜，這隻能從前49個抽屜中取出。而不論從哪個抽屜取出，同一個抽屜里的兩個餘數之和為100，那麼一定有產生這兩個餘數的兩個整數之和能被100整除。

　　(4)證明對任意n+1個整數a₁，a₂，…，a_{n + 1}，存在兩個整數a_i和a_j(i≠j)，使得a_i-a_j能夠被n整除。

　　證明：一個整數除以n的餘數不外乎為0，1，2，…，n-1。n+1個整數a₁，a₂，…，a_{n + 1}除以n則產生n+1個餘數，由於一個整數除以n最多只能產生n個不同的餘數(即n個抽屜)，故根據鴿巢原理，這n+1個餘數中，一定有兩個相等。那麼，產生相等餘數的兩個整數相減，其差一定能被n整除。

　　3.應用於“連續時間”問題

　　(1)某廠在五年期問的每一個月里至少試製一種新產品，每年最多試製19種新產品。試證明：一定存在連續的幾個月，恰好試製24種新產品。

　　證明：設五年期間該廠各個月試製的新產品個數分別為a₁，a₂，…，a₅₉，a₆₀，按題意，構造出數列a_n的前n項和的數列s₁，s₂，…s₅₉，s₆₀，則有：1≤a₁=s₁<s₂<…<s₅₉<s₆₀≤19×5=95，而序列s₁+24，s₂+24，…，s₅₉+24，s₆₀+24也是一個嚴格遞增序列：25≤s₁+24<s₂+24<…<s₅₉+24<s_{60}+24≤95+24=119於是，這120個自然數s₁，s₂，…s₅₉，s₆₀和s₁+24，s₂+24，…，s₅₉+24，s₆₀+24都在區間[1，119]內。在[1，119]內，只有119個自然數，根據抽屜原理，必定存在兩個數相等。

　　上述兩個數列又分別是嚴格單調的，因此必然存在一個i和j，使得s_i=s_j+24。從而，該廠在從第j+1個月起到第i個月的這幾個月時間里，恰好試製了24種新產品。

　　(2)一個孩子每天至少看一個小時電視，總共看7周，但是每周看電視從不超過11小時。證明，存在連續若幹天在此期間這個孩子恰好看電視20個小時。(假設這個孩子每天看電視時間為整數個小時)證明：設這個孩子7周內每天看電視的時間分別為a₁，a₂，…，a₄₉，現在構造出數列{a_n}的前n項和的數列s₁，s₂，…s_{49}，則有：1≤a₁=s₁<s₂<…<s₄₉≤11×7=77，而序列s₁+20，s₂+20，…，s₄9+20也是一個嚴格遞增序列：21≤s_1+20<s_2+20<…<s_{49}+20≤77+20=97於是，這98個自然數s₁，s₂，…s₄₉和s_l+20，s₂+20，…，s₄₉+20都在區間[1，97]內。而在[1，97]內，只有97個自然數，根據抽屜原理，必定存在兩個數相等。而上述兩個數列又分別是嚴格單調的，因此必然存在一個i和j，使得s_i=s_j+20。從而，這個孩子在第j+1天起到第i天的時間里，恰好看電視20個小時。

　　總結：凡遇此類問題都可按照上述方法進行證明。從上面兩題的題目我們可以看出，問題中需要證明的數字(如上面的24和20)加上“在給定時間內能完成任務的最大數字”(如上面的95和77)恰好比“給定時間”的2倍少l。(如：(24+95)+1=60×2，(20+77)+1=49×2)。

　　這是該類問題最重要的特征，因為前兩個數字之和恰好可以看成是抽屜數，而“給定時間”×2可以看成是要被放人抽屜的元素數，抽屜數剛好比元素數少1，則有兩個元素一定會放人同一個抽屜，通過鴿巢原理從而完成對問題的證明。這也是解決此類問題的關鍵所在。

　　4.用於“人的相識”問題

　　(1)證明任意六個人中至少存在三個人或是互相認識，或是互相不認識。

　　證明：在這六個人中任意取定一個人P，則其餘五個人可分為兩類：A={與P認識的人}，B={與P不認識的人}。根據抽屜原理，A和B中至少有一個集合有3個人，不妨設此集合為A，且對於集合A中的3個人a，b，c來說，若他們彼此不認識，則問題得證。否則若a，b，c中有兩個人互相認識，不妨假設這兩個人是a和b，則P，a，b三個人互相認識。

　　若集合B中至少有三個人，用類似的方法也可得到證明。

　　(2)證明在一群n>1個人中，存在兩個人，他們在這群人中有相同個數的熟人。(某人與自己不能算是熟人)證明：在n個人中，每個人所認識的人數只能是0，1，2，…，n-1。

　　如果已知有兩個人認識的人數相等，那麼問題得證。

　　由於某人認識0個人的情況和另一人認識n一1個人的情況不可能同時發生，那麼這n個人所能認識的人數0，1，2，…，n-1也不可能同時存在，即最多只能存在n-1種情況，我們把它看成n-1個抽屜，根據鴿巢原理，n個元素放進n-1個抽屜，則一定有兩個元素在同一個抽屜內，即有兩個人所認識的人數相等。

　　(3)在一個100人的聚會中，每個人都有偶數個(有可能是0個)熟人，證明，在這次聚會上存在3個人有相同個數的熟人。

　　證明：根據題意，每個人所能認識的人數可能為：O，2，4，…，96，98。

　　在這個100人的聚會中，若這50種情況0，2，4，...，96，98都出現，我們假設第1個人認識。個人，第2個人認識2個人，第3個人認識4個人，……，依此類推，第50個人認識98個人，那麼，在餘下的50個人中，如果已知有兩個人有相同個數的熟人，那麼可以得到有3個人認識相同個數的人，問題得證。如果不知道是否還有兩個人有相同、個數的熟人，我們來做下麵的假設：剩下的50個人也是依次認識0，2，4，……，98個人，那麼我們無法證出結論。現在我們來分析假設是否成立。根據以上推導和假設，我們可以得到有兩個人認識0個人，有兩個人認識98個人，對於這兩個認識O個人的人來說，他們自然也不認識那兩個認識98個人的人，而對於那兩個認識98個人的人來說，只能有一個人他們不認識，這就與有兩個人都不認識他們矛盾，所以不可能出現兩個認識0個人的人和兩個認識98個人的人同時存在的情況，故假設不成立。

　　所以剩下的50個人中，最多只能出現認識O，2，4，……，98個人這50種情況的49種，根據鴿巢原理，必然有一種情況要重覆。所以一共存在3個人有相同個數的熟人。

　　若在這l00個人的聚會中，只出現49種或更少的情況，那麼根據鴿巢原理同樣可以得到一定有3個人有相同個數的熟人。