模糊層次分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
模糊層次分析法(fuzzy analytic hierarchy process,FAHP)
目錄 |
模糊層次分析法(FAHP)及計算過程層次分析法(AHP)是20世紀70年代美國運籌學T.L. Saaty教授提出的一種定性與定量相結合的系統分析方法。
該方法對於量化評價指標,選擇最優方案提供了依據,並得到了廣泛的應用。然而, AHP存在如下方面的缺陷:檢驗判斷矩陣是否一致非常困難,且檢驗判斷矩陣是否具有一致性的標準CR < 0. 1缺乏科學依據;判斷矩陣的一致性與人類思維的一致性有顯著差異。在模糊層次分析中,作因素間的兩兩比較判斷時,如果不用三角模糊數來定量化,而是採用一個因素比另一個因素的重要程度定量表示,則得到模糊判斷矩陣。
眾多的風險評價方法中,層次分析法(AHP:the Analytic Hierarchy Process)以其定性和定量相結合地處理各種評價因素的特點,以及系統、靈活、簡潔的優點,受到承包商的特別青睞。其特點是將人的主觀判斷過程數學化、思維化,以便使決策依據易於被人接受,因此,更能適合複雜的社會科學領域的情況。由於AHP在理論上具有完備性,在結構上具有嚴謹性,在解決問題上具有簡潔性,尤其在解決非結構化決策問題上具有明顯的優勢,因此在各行各業得到了廣泛應用。
層次分析法最大的問題是某一層次評價指標很多時(如四個以上),其思維一致性很難保證。在這種情況下,將模糊法與層次分析法的優勢結合起來形成的模糊層次分析法(FAHP),將能很好地解決這一問題。模糊層次分析法的基本思想和步驟與AHP的步驟基本一致,但仍有以下兩方面的不同點:
(1)建立的判斷矩陣不同:在AHP中是通過元素的兩兩比較建立判斷一致矩陣;而在FAHP中通過元素兩兩比較建立模糊一致判斷矩陣
(2)求矩陣中各元素的相對重要性的權重的方法不同
而模糊層次分析法(FAHP)改進了傳統層次分析法存在的問題,提高了決策可靠性。FAHP有一種是基於模糊數,另一種是基於模糊一致性矩陣。
模糊層次分析法的基本思想是根據多目標評價問題的性質和總目標,把問題本身按層次進行分解,構成一個由下而上的梯階層次結構。因此在運用FAHP決策時,大體上可以可分為以下四個步驟。
(1)分析問題,確定系統中各因素之間的因果關係,對決策問題的各種要素建立多級(多層次)遞階結構模型。
(2)對同一層次(等級)的要素以上一級的要素為準則進行兩兩比較,並根據評定尺度確定其相對重要程度,最後據此建立模糊判斷矩陣。
(3)通過一定計算,確定各要素的相對重要度。
(4)通過綜合重要度的計算,對所有的替代方案進行優先排序,從而為決策人選擇最優方案提供科學的決策依據
模糊層次分析法的數學模型[1]
下麵介紹如何建立模糊互補判斷矩陣、模糊互補判斷矩陣權重的計算方法以及模糊互補判斷矩陣的一致性判斷方法。
1、 模糊互補判斷矩陣的建立
在模糊層次分析中,作因素間的兩兩比較判斷時,採用一個因素比另一個因素的重要程度定量表示,則得到的模糊判斷矩陣 ,如果其具
有如下性質:
,如果其具
有如下性質:
1)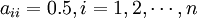 ;
;
2)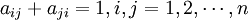 ;
;
則這樣的判斷矩陣稱為模糊互補判斷矩陣。為了使任意兩個方案關於某準則的相對重要程度得到定量描述,通常採用如表1的0.1~0.9標度法給予數量標度。
| 標度 | 定義 | 說明 |
| 0.5 同等重要 | 兩元素相比較, | 同等重要 |
| 0.6 稍微重要 | 兩元素相比較, | 一元素比另一元素稍微重要 |
| 0.7 明顯重要 | 兩元素相比較, | 一元素比另一元素明顯重要 |
| 0.8 重要得多 | 兩元素相比較, | 一元素比另一元素重要得多 |
| 0.9 極端重要 | 兩元素相比較, | 一元素比另一元素極端重要 |
| 0.1,0.2,0.3,0.4 | 反比較 | 若元素ai與元素aj相比較得到判斷rii,則原素a_i與元素ai相比較得到的判斷為rji=1-rij |
aii = 0.5表示因素與自己相比同樣重要;若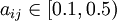 ,則表示因素xj比xi重要;若
,則表示因素xj比xi重要;若![a_{ij} \in [0.5,0.9]](/w/images/math/d/a/4/da4cc5ddc34bb2c33c2b76a16f32a393.png) ,則表示因素xi比xj重要。
,則表示因素xi比xj重要。
依據上面的數字標度,因素a1,a2,…,an相互進行比較,則得到如下模糊互補判斷矩陣
A= (1)
(1)
2、模糊互補判斷矩陣的權重公式
推導出求解模糊互補判斷矩陣權重的一種通用公式,該公式充分包含了模糊一致性判 斷矩陣的優良特性及其判斷信息,計算量小且便於電腦編程實現,為實際應用帶來了極大方便。該求解模糊互補判斷矩陣權重的公式如下:
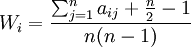 (2)
(2)
3、模糊互補判斷矩陣的一致性檢驗方法
由式(2)得到的權重值是否合理,還應該進行比 較判斷的一致性檢驗。當偏移一致性過大時,表明此時將權向量的計算結果作為決策依據是不可靠的。推導出用模糊判斷矩陣的相容性來檢驗其一致性原則的方法。
定義1:設矩陣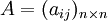 和
和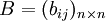 均為模糊判斷矩陣,稱
均為模糊判斷矩陣,稱
 (3)
(3)
為A和B的相容性指標。
定義2:設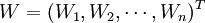 是模糊判斷矩陣A的權重向量,其中
是模糊判斷矩陣A的權重向量,其中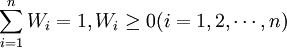 ,令
,令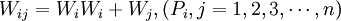 ,則稱n階矩陣:
,則稱n階矩陣:
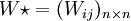 (4)
(4)
為判斷矩陣A的特征矩陣。對於決策者的態度A,當相容性指標 時,認為判斷矩陣為滿意一致性的。A越小表明決策者對模糊判斷矩陣的一致性要求越高,一般可取A=0.1。
時,認為判斷矩陣為滿意一致性的。A越小表明決策者對模糊判斷矩陣的一致性要求越高,一般可取A=0.1。
對於實際的問題,一般都是由多個(設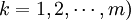 專家給出同一因素集X上的兩兩比較判斷矩陣
專家給出同一因素集X上的兩兩比較判斷矩陣
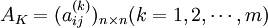
它們均是模糊互補判斷矩陣,則可分別得到權重集的集合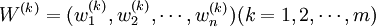
則進行模糊互補判斷矩陣的一致性檢驗,要做以下兩方面的工作:
1)檢驗m個判斷矩陣Ak的滿意一致性: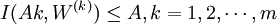
2)檢驗判斷矩陣間的滿意相容性:
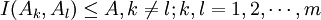 可以證明在模糊互補判斷矩陣
可以證明在模糊互補判斷矩陣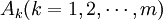 是一致可接受的情況下,它們的綜合判斷矩陣也是一致可接受的。權重向量表達式:
是一致可接受的情況下,它們的綜合判斷矩陣也是一致可接受的。權重向量表達式:
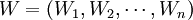 (5)
(5)
式(5)中: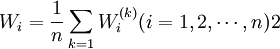
即只要當1)和2)兩條滿足時,m個權重集的均值作為因素集X的權重分配向量是合理和可靠的。
- ↑ 姬東朝,宋筆鋒,喻天翔.基於模糊層次分析法的決策方法及其應用.火力與指揮控制.第32捲第11期.2007年11月







