風險型決策
出自 MBA智库百科(https://wiki.mbalib.com/)
風險型決策(Risk Type Decision/decision making under risk)
目錄 |
風險型決策:是指決策者對決策對象的自然狀態和客觀條件比較清楚,也有比較明確的決策目標,但是實現決策目標必須冒一定風險。
文字風險型決策是指每個備選方案都會遇到幾種不同的可能情況,而且已知出現每一種情況的可能性有多大,即發生的概率有多大,因此在依據不同概率所擬定的多個決策方案中,不論選擇哪一種方案,都要承擔一定的風險。
先驗概率:根據過去經驗或主觀判斷而形成的對各自然狀態的風險程度的測算值。
自然狀態:指各種可行方案可能遇到的客觀情況和狀態。
損益矩陣:一般有三部分組成:可行方案、自然狀態及其發生的概率、各種行動方案的可能結果。把這三部分內容在一個表上表現出來,這個表就是損益矩陣表。
常用的方法有:以期望值為標準的決策方法、以等概率(合理性)為標準的決策方法、以最大可能性為標準的決策方法等。
- (一)各種方法描述
以期望值為標準的決策方法:以收益和損失矩陣為依據,分別計算各可行方案的期望值,選擇其中期望收益值最大(或期望損失值最小)的方案作為最優方案。
設E(di)表示第 個方案的期望值;xij表示採取第i個方案,出現第j種狀態時的損益值;P(θj) 表示第j種狀態發生的概率,總共可能出現m種狀態,則期望損益的計算公式為: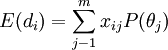
以等概率(合理性)為標準的決策方法:由於各種自然狀態出現的概率無法預測,因此假定幾種自然狀態的概率相等,然後求出各方案的期望損益值,最後選擇收益值最大(或期望損失值最小)的方案作為最優決策方案。
以最大可能性為標準的決策方法:此方法是以一次試驗中事件出現的可能性大小作為選擇方案的標準,不是考慮其經濟的結果。
- (二)各種方法的適用場合
1.以期望值為標準的決策方法一般適用於幾種情況:
(1)概率的出現具有明顯的客觀性質,而且比較穩定;
(2)決策不是解決一次性問題,而是解決多次重覆的問題;
(3)決策的結果不會對決策者帶來嚴重的後果。
2.以等概率(合理性)為標準的決策方法適用於各種自然狀態出現的概率無法得到的情況。
3.以最大可能性為標準的決策方法適用於各種自然狀態中其中某一狀態的概率顯著地高於其它方案所出現的概率,而期望值相差不大的情況。
(一)簡述
決策樹是對決策局面的一種圖解。它是把各種備選方案、可能出現的自然狀態及各種損益值簡明地繪製在一張圖表上。用決策樹可以使決策問題形象化。
(二)決策樹圖的製作步驟
1.繪出決策點和方案枝,在方案枝上標出對應的備選方案;
2.繪出機會點和概率枝,在概率枝上標出對應的自然狀態出現的概率值;
3.在概率枝的末端標出對應的損益值,這樣就得出一個完整的決策局面圖。
(三)決策樹圖的分析
決策樹圖的分析程式是先從損益值開始由右向左推導,稱為反推決策樹法。
(一)簡述
在決策過程中,自然狀態出現的概率值變化會對最優方案的選擇存在影響。概率值變化到什麼程度才引起方案的變化,這一臨界點的概率稱為轉折概率。對決策問題做出這種分析,就叫做敏感性分析,或者叫做靈敏度分析。
(二)敏感性分析的步驟
1.求出在保持最優方案穩定的前提下,自然狀態出現概率所變動的容許範圍;
2.衡量用以預測和估算這些自然狀態概率的方法,其精度是否能保證所得概率值在此允許的誤差範圍內變動;
3.判斷所作決策的可靠性。
- 一、效用概率決策
效用概率決策方法是以期望效用值作為決策標準的一種決策方法。
效用:決策人對於期望收益和損失的獨特興趣、感受和取捨反應就叫做效用。效用代表著決策人對於風險的態度,也是決策人膽略的一種反映。效用可以通過計算效用值和繪製效用曲線的方法來衡量。
效用曲線:用橫坐標代表損益值,縱坐標代表效用值,把決策者對風險態度的變化關係繪出一條曲線,就稱為決策人的效用曲線。
連續性變數的風險型決策方法是解決連續型變數,或者雖然是離散型變數,但可能出現的狀態數量很大的決策問題的方法。連續性變數的風險型決策方法可以應用邊際分析法和標準正態概率分佈等進行決策。
方法的思想:設法尋找期望值作為一個變數隨備選方案依一定次序的變化而變化的規律性,只要這個期望值變數在該決策問題定義的區間內是單峰的,則峰值處對應的那一個備選方案就是決策問題的最優方案。這個方法類似於經濟學中的邊際分析法。
- 三、馬爾科夫決策
馬爾科夫決策方法就是根據某些變數的現在狀態及其變化趨向,來預測它在未來某一特定期間可能出現的狀態,從而提供某種決策的依據。馬爾科夫決策基本方法是用轉移概率矩陣進行預測和決策。
轉移概率矩陣:矩陣各元素都是非負的,並且各行元素之和等於1,各元素用概率表示,在一定條件下是互相轉移的,故稱為轉移概率矩陣。如用於市場決策時,矩陣中的元素是市場或顧客的保留、獲得或失去的概率。P(k)表示 步轉移概率矩陣。








請問有案例嗎