連續性變數風險型決策
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
連續性變數的風險型決策方法是解決連續型變數,或者雖然是離散型變數,但可能出現的狀態數量很大的決策問題的方法。連續性變數的風險型決策方法可以應用邊際分析法和標準正態概率分佈等進行決策。
方法的思想:設法尋找期望值作為一個變數隨備選方案依一定次序的變化而變化的規律性,只要這個期望值變數在該決策問題定義的區間內是單峰的,則峰值處對應的那一個備選方案就是決策問題的最優方案。這個方法類似於經濟學中的邊際分析法。
邊際利潤:指存有並賣出一追加單位產品所得到的利潤值。
期望邊際利潤:是邊際利潤乘以其中的追加產品能被賣出的概率。
邊際損失:指由於存有一追加單位產品而賣不出去所造成的損失值。
期望邊際損失:是邊際損失乘以其中的追加產品賣不出去的概率。
- (一)邊際分析法的應用
令期望邊際利潤等於期望邊際損失,求出轉折概率,根據轉折概率對應結果進行決策。
- (二)應用標準正態概率分佈進行決策
設有一生產銷售問題的風險型決策,如果滿足下列兩個條件,即:
1、該決策問題的自然狀態(市場需求量)為一連續型的隨機變數x,其概率密度為f(x);
2、備選方案d1,d2,...,dm分別表示生產(或存有)數量為1,2,...,m單位的某種產品或商品。
那麼,該風險型決策取得最大期望利潤值的方案dx,其所代表生產(存有)的單位產品數量k(最佳方案)由下式決定:
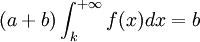
其中:a為邊際利潤值,即生產並賣出一追加單位產品所獲得的利潤值;b為邊際損失值,即存有一追加單位產品而賣不出去所造成的損失值。







