期初年金終值
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
期初年金終值(Amount of Annuity Due)
目錄 |
[編輯]
期初年金終值是指每期期初發生的分次款以及由這些分次款複利累積的總和。
[編輯]
![S=R(\frac{1+i}{i})[(1+i)^n-1]](/w/images/math/a/4/6/a4681cb35562cf83683302f67cfec64b.png)
即: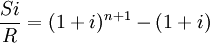
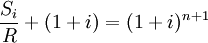
兩邊取對數,得
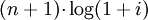
![=\log[\frac{Si}{R}+(1+i)]](/w/images/math/6/b/6/6b6b0d5fca23b7dc26ffe585c18a0b17.png)
![n+1=\frac{\log[\frac{Si}{R}+(1+i)]}{\log(1+i)}](/w/images/math/9/6/0/96085d6604ba0d15cd4e1c2b7a94abc3.png)
![n=\frac{\log[\frac{Si}{R}+1+i]}{\log(1+i)}-1](/w/images/math/2/2/1/221b385d10f645c84cd8fea3032f8f8b.png)
![=\frac{\log[i(\frac{S}{R}+1)+1]}{\log(1+i)}-1](/w/images/math/2/0/7/207095615c6d14c88fca50e5cb246a20.png)
[編輯]
計算期初年金終值的舉例 [1]
例:1
每年初存入銀行10000元,按年利率5%複利計息,問儲積至本利和為58019元需要幾年?
![n=\frac{\log[1+(\frac{58019}{10000}+1)\times5%]}{\log(1+5%)}-1](/w/images/math/a/a/8/aa8f395796810cbf85edbfa917ae54fe.png)

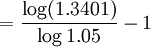
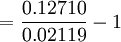
= 5(年)
即5年期末可得本利和58019元。
例:2
每年初存入銀行10000元,按年利率5%複利計算,問5年未可得本利和多少?
解:已知T=10000,i=5%,n=5
本利和
![S=R(1+I)[\frac{(1+i)^n-1}{i}]](/w/images/math/f/a/7/fa71bda36075b54e73df795a3754bf0c.png)
![=10000\times(1+5%)[\frac{(1+5%^5-1)}{5%}]](/w/images/math/4/6/f/46f68a633e3dd9909162ed25e9f27ae8.png)
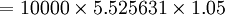
= 58019元。
[編輯]
[編輯]
- ↑ 許友梅 張元奎 羅勛才 施潮.管理知識手冊.知識出版社,1983年09月第1版.







