期初年金终值
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
期初年金终值(Amount of Annuity Due)
目录 |
[编辑]
期初年金终值是指每期期初发生的分次款以及由这些分次款复利累积的总和。
[编辑]
![S=R(\frac{1+i}{i})[(1+i)^n-1]](/w/images/math/a/4/6/a4681cb35562cf83683302f67cfec64b.png)
即: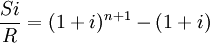
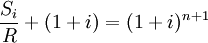
两边取对数,得
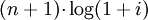
![=\log[\frac{Si}{R}+(1+i)]](/w/images/math/6/b/6/6b6b0d5fca23b7dc26ffe585c18a0b17.png)
![n+1=\frac{\log[\frac{Si}{R}+(1+i)]}{\log(1+i)}](/w/images/math/9/6/0/96085d6604ba0d15cd4e1c2b7a94abc3.png)
![n=\frac{\log[\frac{Si}{R}+1+i]}{\log(1+i)}-1](/w/images/math/2/2/1/221b385d10f645c84cd8fea3032f8f8b.png)
![=\frac{\log[i(\frac{S}{R}+1)+1]}{\log(1+i)}-1](/w/images/math/2/0/7/207095615c6d14c88fca50e5cb246a20.png)
[编辑]
计算期初年金终值的举例 [1]
例:1
每年初存入银行10000元,按年利率5%复利计息,问储积至本利和为58019元需要几年?
![n=\frac{\log[1+(\frac{58019}{10000}+1)\times5%]}{\log(1+5%)}-1](/w/images/math/a/a/8/aa8f395796810cbf85edbfa917ae54fe.png)

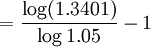
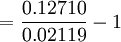
= 5(年)
即5年期末可得本利和58019元。
例:2
每年初存入银行10000元,按年利率5%复利计算,问5年未可得本利和多少?
解:已知T=10000,i=5%,n=5
本利和
![S=R(1+I)[\frac{(1+i)^n-1}{i}]](/w/images/math/f/a/7/fa71bda36075b54e73df795a3754bf0c.png)
![=10000\times(1+5%)[\frac{(1+5%^5-1)}{5%}]](/w/images/math/4/6/f/46f68a633e3dd9909162ed25e9f27ae8.png)
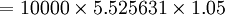
= 58019元。
[编辑]
[编辑]
- ↑ 许友梅 张元奎 罗勋才 施潮.管理知识手册.知识出版社,1983年09月第1版.







