有限單元法
出自 MBA智库百科(https://wiki.mbalib.com/)
有限單元法(Finite Element Method)
目錄 |
什麼是有限單元法[1]
有限單元法是指將連續的介質(如零件、結構等)看作由在有限個節點處聯接起來的有限個小塊(稱為元素)所組成,然後對每個元素通過取定的插值函數,將其內部每一點的位移(或應力)用元素節點的位移(或應力)來表示,隨後根據介質整體的協調關係,建立包括所有節點的這些未知量的聯立方程組,最後用電腦求解該聯立方程組,以獲得所需的解答。當元素足夠“小”時,可以得到十分精確的解答。
有限單元法的起源[2]
1952年,波音公司Jon Turner領導一個項目小組分析三角翼強度時,發現採用小的三角形組裝機翼,可以準確地計算出機翼變形。他稱這種方法為直接剛度法,併發表了著名的學術論文——Turner MJ,Clough RW,Martin HC,Topp LJ.Stiffness and deflec—tion analysis ofcomplex structures.J Aero Sci 1956;23:805-23,這是有限單元法的雛形。1965年“有限元”這個名詞第一次出現。有限元的核心思想是結構的離散化,就是將實際結構假想地離散為有限數目的規則單元組合體,使得實際結構的物理性能可以通過對離散體進行分析,得出滿足工程精度的近似結果來替代對實際結構的分析,這樣可以解決很多實際工程需要解決而理論分析又無法解決的複雜問題。
理論解析方法提供了固體、流體、熱、電磁領域的完美求解方程和邊界條件,但對於複雜形體的不能得到解析解。複雜形體是簡單形體堆積的結果,而簡單的形體總是可以得到解析結果,比如方塊或四面體。有限元方法是一種模擬在確定的荷載條件下的結構響應的方法,就是把複雜形體用大量簡單形體堆積,先處理簡單的形體,再推演處理複雜的形體,使得複雜問題簡單化。每一個簡單形體稱為一個單元,單元越小,堆積出來的形狀越接近真實形體。用有限元方法解決問題時首先將複雜的形體劃分成網格,每個網格就是一個單元,網格分得越細,計算結果越精確。
有限元方法在工程上得到了廣泛應用,經歷了幾十年的發展歷史,理論和演算法都日趨完善。隨著電腦技術的普及和計算速度的不斷提高,有限元分析在工程設計和分析中得到了越來越廣泛的重視,已經成為解決複雜的工程分析計算問題的有效途徑。現在從汽車到太空梭幾乎所有的設計製造都已離不開有限元分析計算,其在機械製造、材料加工、航空航天、汽車、土木建築、電子電氣、國防軍工、船舶、鐵道、石化、能源、科學研究等各個領域的廣泛使用已使設計水平發生了質的飛躍。隨後,經過數學家從理論上的完善,使有限元法不斷發展,並逐漸應用於求解航空、航天、機械、電子、船舶、土木等眾多的工程問題。
有限單元法的優缺點[3]
1.有限單元法的優點
(1)因為單元能按各種不同的連接方式組合在一起,且單元本身又可以有不同的形狀。所以,有限單元法可以模擬各種幾何形狀複雜的結構,得出其近似解。
(2)有限單元法的解題步驟可以系統化、標準化,能夠開發出靈活通用的電腦程式,使得其能夠廣泛地應用於各種場合。
(3)邊界條件是在建立結構總體剛度方程後再引入的,邊界條件和結構模型具有相對獨立性,可以從其他CAD軟體中導入創建好的模型。
(4)有限單元法不需要適用於整個結構的插值函數,而是每個單元本身有各自的插值函數。這就使得數學處理比較方便,對複雜形狀的結構也能適用。
(5)有限單元法很容易處理非均勻連續介質。
(6)可以求解非線性問題。
(7)可以進行耦合場分析。
(8)有限單元法可以與優化設計方法相結合,以便發揮各自的優點。
2.有限單元法的缺點
(1)有限單元計算,尤其是複雜問題的分析計算,所耗費的計算時間、記憶體和磁碟空間等計算資源是相當驚人的。
(2)對無限求解域問題沒有較好的處理方法。
(3)儘管現有的有限元軟體多數都使用了網格自適應技術,但在具體應用時,採用什麼類型的單元、多大的網格密度等都要完全依賴於使用者的經驗。在實際應用中,經常採用網格密度加大一倍的辦法,然後比較兩次分析的結果來考察分析的精度,這勢必進一步增大了計算資源的耗費量。
有限單元法的分類[4]
在有限單元法的算式推導中並不一定要取節點位移為基本未知量,也可以取節點力為未知量。由於所取未知量的不同,有限單元法可以分為:
位移法——以節點位移作為基本未知量;
力法——以節點力作為基本未知量;
混合法——以一部分節點位移,一部分節點的力作為基本未知量。
由於位移法的基本未知量為位移分量,比力法的基本未知量應力分量的數量少,使用經典力學的基本方程就可以求解,而且位移法得出的方程組和計算程式也簡單,故得到廣泛應用。
從公式推導方法來看,有限單元法也可以分為三類:
直接法——把各個單元的節點力與節點位移的關係式,按照一定的次序進行迭加,而求出整個物體的方程組的方法,稱為直接法。這種方法比較直觀,易於理解。但僅適用於求解比較簡單的問題。直接剛度法就是其典型代表。
變分法——應用變分原理,把有限單元法歸結為求泛函的極值問題。對於固體力學來講,就是應用最小能量原理來求整個物體的方程組。變分原理的應用,使有限單元法建立在更加堅實的數學基礎上,並擴大了其應用範圍。
加權餘數法——即迦遼金法。這種方法可以直接從基本微分方程導出有限元列式,而不需要利用泛函的概念。因此,對於不存在泛函的工程領域也可採用,從而進一步擴大了有限單元法的應用範圍。
有限單元法的應用[2]
有限單元法是利用電子電腦進行數值模擬的方法。有限元分析技術可以實現:
(1)發現產品潛在的問題及先天缺陷,創造品質優異的產品。
(2)進行風險評估與預測,提高產品和工程的可靠性,降低風險。
(3)經過對比分析計算,採用優化設計方案,降低產品成本。
(4)縮短產品投向市場的時間。
(5)減少物理試驗次數,對大量情況進行快速有效模擬試驗分析,從而減少試驗經費。
(6)模擬不適合在原型上進行試驗的設計,例如器官移植、人造膝蓋等。
(7)模擬無法看到或重現的場景,如事故分析及調查。
有限單元法的常用領域[5]
表1 有限單元法常用領域一覽表
| 應用領域 | 場變數 | 作用量 | 性質矩陣 |
| 結構力學 | 位移或/和應力 | 機械荷載、施加的位移 | 彈性或彈塑性剛度 |
| 熱彈性力學 | 溫度、位移或應力 | 機械荷載、施加的位移、溫度 | 彈性或彈塑性剛度,膨脹繫數,熱傳導繫數 |
| 黏彈性力學 | 溫度或應力 | 機械荷載、施加的位移、溫度 | 鬆弛剛度 |
| 熱傳導 | 溫度 | 熱流量、邊界溫度 | 熱傳導繫數、比熱 |
| 流體力學 | 位移、速度或位勢 | 速度、應力、壓強、重力 | 黏性 |
| 流動彈性力學 | 位移、速度、位勢 | 機械荷載、位移 | 質量、剛度、黏性 |
| 擴散、對流 | 濃度函數 | 濃度 | 彌散繫數、孔隙率 |
有限單元法的分析步驟[5]
(1)連續體的離散化。也就是將給定的物理系統分割成等價的有限單元系統。一維結構的有限單元為線段,二維連續體的有限單元為三角形、四邊形,三維連續體的有限單元可以是四面體、長方體或六面體,不同類型的單元有其不同的優缺點。根據實際應用,還可以發展更多的單元,不同類型單元通過不同有限元節點具體表達。需要決定單元的類型、數目、大小和排列方式,以便能夠合理有效地表示給定的物理系統。
(2)選擇位移模型。假設的位移函數或模型只是近似地表示了真實位移分佈。通常假設位移函數為多項式,最簡單情況為線性多項式。實際應用中,沒有一種多項式能夠與實際位移完全一致。用戶所要做的是選擇多項式的階次,以使其在可以承受的計算時間內達到足夠的精度。此外,還需要選擇表示位移大小的參數,它們通常是節點的位移,但也有可能包括節點位移的導數。
(3)用變分原理推導單元剛度矩陣。單元剛度矩陣是根據最小位能原理或者其它原理,由單元材料和幾何性質導出的平衡方程繫數構成的。單元剛度矩陣將節點位移和節點力聯繫起來,物體受到的分佈力變換為節點處的等價集中力。剛度矩陣k、節點力矢量f和節點位移矢量q的平衡關係表示為線性代數方程組:kp=f
(4)集合整個離散化連續體的代數方程。也就是把各個單元的剛度矩陣集合成整個連續體的剛度矩陣,把各個單元的節點力矢量集合為總的力和載荷矢量。最常用的原則是要求節點能互相連接,即要求所有與某節點相關聯的單元在該節點處的位移相同。但是最近研究表明:該原則在某些情況下並不是必需的。總剛度矩陣K、總載荷矢量F以及整個物體的節點位移矢量Q之間構成整體平衡,其聯立方程為:KQ=F
這樣得出物理系統的基本方程後,還需要考慮其邊界條件或初始條件,才能夠使得整個方程封閉。如何引入邊界條件依賴於對系統的理解。
(5)求解位移矢量。即求解上述代數方程,這種方程可能簡單,也可能很複雜,比如對非線性問題,在求解的每一步都要修正剛度矩陣和載荷矢量。
(6)由節點位移計算出單元的應變和應力。視具體情況,可能還需要計算出其他一些導出量。
在實際工作中,上述有限元分析只是在電腦軟體處理中的步驟(有限元程式);要完成工程分析,還需要更多的前處理和後處理,完整的有限元分析流程圖如圖1所示。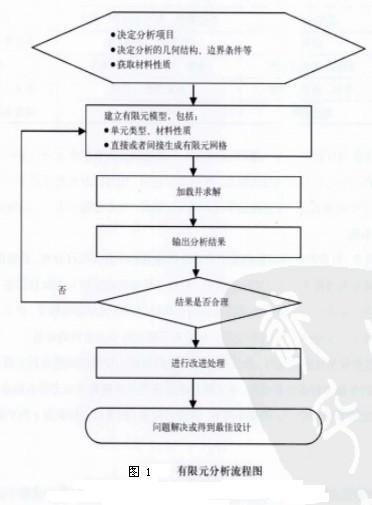
有限元法在現代設計過程中的作用[4]
1.應力和變形的計算,有利於提高產品的安全可靠性
傳統設計方法中,一般採用安全繫數法來保證結構使用的安全性,這樣做的原因有三個:設計時對象的真實載荷無法準確把握;由於問題的複雜性,傳統設計解析法無法對給定載荷條件下的應力分佈及水平進行準確計算;真實結構的材料物理性能可能跟設計計算值有出入。傳統安全繫數法的不足在於,一方面計算誤差大,造成浪費;另一方面又不能確保全全。
有限單元法的最初應用,主要解決的是給定載荷條件下求取結構的應力場及應力水平的問題。顯然,有限元法的應用,一方面消除了設計過程中的一個不確定環節,另一方面,在準確把握載荷與應力應變關係的基礎上,又可以適當地採用小的安全繫數來進行設計,從而有效降低成本。
2.產品性能與結構優化模擬分析,縮短新產品開發周期與研製費用
一般地,新產品的開發過程,都有樣機試製及樣機性能實驗環節,而且需要進行多次試製才能找到最佳方案。而採用有限單元法進行產品性能、結構優化模擬研究並與物理模擬相結合的方法則可有效減少性能測試樣品的數量以及方案尋優的次數,從而有效縮短新產品開發周期與研製費用。如汽車的碰撞性能模擬等。
3.工程問題的理論性研究,為產品的設計與產品使用提供理論依據
有限單元法適用於各種物理問題模擬的強大功能,使其成為到目前為止工程問題理論研究最強大的工具之一,也是現代設計過程及產品使用獲得理論依據的最重要的手段之一。例如,軋鋼過程的模擬研究,一方面是軋機設計過程載荷及工藝參數確定的基礎,另一方面又是設備運行的工藝參數優化的基礎。
邊界單元法與有限單元法的比較[6]
力學問題的求解可歸結為一組偏微分方程的定解問題。由於數學上的困難,只有很少量簡單的問題才能找到問題的解析解,而實際工程問題往往又比較複雜,而且多數是非線性問題,這使得數值計算方法非常重要。
目前,工程問題的力學分析使用最廣泛的數值計算方法是有限單元法。這一方面歸因於有限單元法理論完備,方法本身對各類工程問題有廣泛的適用性;另一方面是基於有限單元法的大型商業分析軟體開發比較成熟。這兩個方面的推動使得有限單元方法成為各行各業分析複雜工程問題的主要手段之一。作為力學專業的學生,掌握有限單元法的理論基礎和演算法原理,熟練使用至少一款主流有限元分析軟體應該是最基本的要求。
然而,任何一種方法都有其優勢也有局限性。有限元法是基於求解域內部網格的一種數值方法。這一特點使其在處理一些問題時也遇到困難。例如,在金屬成型、優化計算、裂紋擴展以及滲流等動邊界問題中,網格會產生嚴重畸變、重疊等問題,影響求解精度甚至無法計算。另外,在處理地下工程、地基基礎等無限、半無限域問題時,有限元法需要人為給定無擾動有限邊界,這對問題的建模和解的唯一性帶來一定程度的不確定性。
邊界單元法的主要特點可概括為:(1)只在求解域的邊界劃分網格;(2)在求解域內採用基本解,使得域內場方程得到精確滿足。這些特點使得邊界單元法與有限單元法相比具有以下優勢。
(1)由於只需在域邊界離散,使得問題的維數下降,降低了求解規模。例如,對一個三維彈性力學問題,只需在求解域的錶面劃分二維單元;對平面問題,只需在域邊界劃分一維線單元。因此,邊界單元法的建模、數據準備以及計算工作量與有限單元法相比大大降低。
(2)由於只在邊界離散,處理動邊界問題非常方便。例如,在裂紋擴展問題模擬中,有限單元法需要在裂紋的每個擴展步生成新的裂紋邊界面、調整裂紋尖端附近的網格,而這項工作往往是非常困難的。相反,邊界單元法由於可以事先在裂紋擴展路徑上劃分好單元,在每一擴展步只需對這些裂紋單元的位置進行修正,而無需大規模調整網格。
(3)由於採用基本解,控制方程在域內精確滿足,使得近似計算的誤差實際上只發生在邊界。因此,邊界元法的求解精度相對較高,非常適合求解應力集中問題。
(4)由於採用基本解,非常適合求解無限、半無限域問題。這一特點使得邊界元法在聲場、電磁場問題分析中有比有限元法更為廣泛的應用。
(5)位移解法的有限單元法以位移為基本未知量,只對位移場插值,求出位移後,對其求導得到應變,再由應力-應變關係計算應力。因此,應力場精度比位移場低。而邊界單元法中,以邊界上的位移和麵力為未知數,兩者同時單獨插值,同時求解,解的精度是相同的,在計算域內點的應力時精度也不會降低。
(6)由於在邊界上位移和麵力同時單獨插值,在處理考慮摩擦的接觸問題時比有限元法方便許多。
邊界單元法也存在弱點,主要表現為:
(1)採用的基本解導致奇異積分出現,使得數值計算時需要處理奇異積分。
(2)所形成的繫數矩陣為非對稱滿陣,限制瞭解題規模和速度。
(3)在處理彈塑性問題等非線性問題時會出現域內積分,削弱了其只在邊界離散形成的優勢。
(4)對於一些非均質等問題,很難求得問題的基本解。
邊界單元法是針對一些特定問題對有限單元法的有益補充。







