最大期望收益法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　最大期望收益法是指用未來收益的期望值作為未來真實收益的代表，並據此利用凈現值法、收益率法等進行投資決策。最大期望收益法是在風險條件下(未來收益不確定條件下)簡單易行和常用的決策方法。

　　1.求收益值

　　實例分析：某商店銷售羽絨服，羽絨服成本為100元，銷價為150元，若今冬售出一件則會贏利50元，今冬售不出則會損失10元。現根據對市場需求的初步瞭解和以往的經驗，估計今冬售出100件的可能性為20％；售出150件的可能性為50％；銷出180件的可能性為30％，看商店應選擇何種進貨方案為宜。

　　根據所給條件，編製決策收益見下表：

　　根據上表中數據，求出各收益值為：

　　O₁₁=50\times100=5000</math>(元)(表示進貨100件，每件利潤50元，全部售出則商店收益為5000元)。

　　O₂₁=50\times100-(150-100)\times10=4500</math>(元)(表示進貨150件，售出100件，剩餘50件。獲利50×100=5000元，損失(150-100)×10=500元，商店實際收益5000-500=4500元)

　　O₃₁=50×100-(180-l00)×10=4200(元)(表示進貨．180件，售出100件，剩餘80件。獲利50×100=5090無，損失(180-100)×10=800元，商店實際收益5000—800=4200元) ‘

　　O₁₂=50×100=5000(元)(表示進貨100件，市場需求150件，但因進貨量已定，所以商店收益只能是50×100=5000元) ．

　　O₂₂=50×150=7500〔元)(表示進貨150件，每件利潤50元，全部售出，商店收益為7500元)

　　O₃₂=50×150-(180-150)×10=7200(元)(表示進貨180件，售出150件，剩餘30件。獲利50×150=7500元，損失(180一150)×lo=300元，商店實際收益7500“300=7200(元)

　　O₁₃=50×100=5000(元)(表示進貨100件，市場需求180件，但因進貨量已定，所以商店收益只能是50×100=5000元)

　　O₂₃=50×150於7500(元)(表示進貨150件，市場需求180件，但因進貨量已定，所以商店收益只能是50×150=7500元)

　　O₃₃=50×180=9000(元)(表示進貨180件，每件利潤50元，全部售出，商店收益為9000元)

　　2.求期望收益值

　　各方案的期望收益值，是在決策收益表的基礎上，將各方案自然狀態發生的概率值乘以不同自然狀態下收益值所得積之總和。

　　期望收益值的計算公式為：

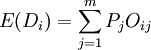
　　式中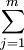：——第i種決策方案中的期望受益值；

　　P_j第j個自然狀態的概率；

　　O_ij第i種決策方案中第j種自然狀態的收益值。

　　此例各方案的期望收益值為：

　　100件計劃方案的期望收益值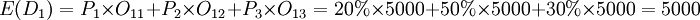(元)

　　150件計劃方案的期望收益值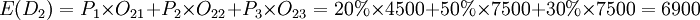(元)

　　180件計劃方案的期望收益值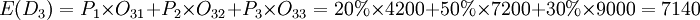(元)

　　此例中，max[E(D₃)] = 7140(元)，即180件計劃方案的期望收益值為最大，商店決策時應考慮選擇此方案為最優方案。