序數效用論
出自 MBA智库百科(https://wiki.mbalib.com/)
序數效用論(Theory Of Ordinal Utility)
目錄 |
序數效用論是由英國經濟學家約翰·希克斯提出,是消費者行為理論中兩個重要的理論之一,序數效用論是為了彌補基數效用論的缺點而提出來的另一種研究消費者行為的理論。
1934年,希克斯和艾倫在《價值理論的再思考》這篇著名論文中提出:效用作為一種心理現象是無法計量的,因為不可能找到效用的計量單位;他們運用埃奇沃思發明的“無差異曲線”對效用進行了重新詮釋,認為消費者在市場上所做的並不是權衡商品效用的大小而只是在不同的商品之間進行排序。這就是所謂的序數效用論。序數效用論力圖避免效用可以直接被計量這種尷尬的假設,併為經濟學提供了一種新的分析方法,即無差異曲線分析。
序數效用論的基本觀點是:效用作為一種心理現象無法計量,也不能加總求和,只能表示出滿足程度的高低與順序,因此,效用只能用序數(第一、第二、第三……)來表示。例如,消費者消費了巧克力與唱片,他從中得到的效用是無法衡量,也無法加總求和的,更不能用基數來表示,但他可以比較從消費這兩種物品中所得到的效用。如果他認為消費l塊巧克力所帶來的效用大於消費唱片所帶來的效用,那麼就叫一塊巧克力的效用是第一,唱片的效用是第二。
序數效用論採用無差異曲線的分析法。序數效用論用消費者偏好的高低來表示滿足程度的高低。該理論建立在以下假定上:
1、完備性,即指對每一種商品都能說出偏好順序。
2、可傳遞性,即消費者對不同商品的偏好是有序的,連貫一致的。若A大於B,B大於C,則A大於C。
3、不充分滿足性,即消費者認為商品數量總是多一些好。
序數效用論採用無差異曲線分析法來考察消費者行為,併在此基礎上推導需求曲線。而基數效用論採用邊際效用的分析法。物的效用向量可以表示為: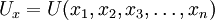 。向量的模長可以直接比較,這是基數效用論的方法;多個向量可以複合成一個總的向量,或者一個總的向量可以分解成多個、多組向量,這是序數效用論的方法。下表給出兩種理論的具體區別:
。向量的模長可以直接比較,這是基數效用論的方法;多個向量可以複合成一個總的向量,或者一個總的向量可以分解成多個、多組向量,這是序數效用論的方法。下表給出兩種理論的具體區別:
| 效用理論類型 | 主要觀點 | 假設條件 | 分析工具 | 經濟學家 |
|---|---|---|---|---|
| 基數效用論 | 效用可計量 | 苛刻 | 邊際效用 | 馬歇爾 |
| 序數效用論 | 效用可比較 | 寬鬆 | 無差異曲線 | 希克斯 |
基數效用論和序數效用論,是消費者行為理論中兩個重要的理論。序數效用論的緣起,在於分析效用會相互影響的不同商品之間的關係(由Jevons等人的邊際革命所推廣的基數效用論一開始假設商品之間的效用沒有相互影響,因而無法研究有關聯的商品之間的關係,於是Pareto從Edgeworth那裡借用了無差異曲線,用以說明兩種商品之間的關係)。從這裡可以知道,無差異曲線最早是從效用曲線得來的,而效用曲線本來是基數效用論中的概念。
無差異曲線是表示能給消費者帶來同等效用水平或滿足程度的兩種商品的不同數量的各種組合的。無差異曲線相對應的效用函數:U=f(Xl、X2),其中,Xl和X2分別為商品1和商品2的數量;U是常數,表示某個效用水平。無差異曲線的特殊形狀:
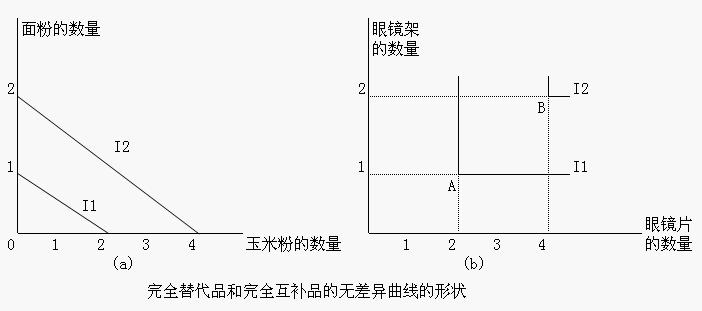
1、完全替代品情況
完全替代品指兩種商品之間的替代比例是固定不變的情況。因此,在完全替代的情況下,兩商品之間的邊際替代率MRS12就是一個常數,相應的無差異曲線是一條斜率不變的直線。
2、完全互補品情況
完全互補品指兩種商品必須按固定不變的比例同時被使用的情況。因此,在完全互補的情況下,相應的無差異曲線為直角形狀。
該分析假定消費者購買兩種商品X1、X2,且給定一個不變的效用水平U0,則效用函數為:
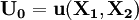 (1-1)
(1-1)
式(1-1)表示給定的效用水平U0可以從X1和X2的不同組合中獲得,由於X1的減少必須由X2的增加來彌補,所以ΔX2 / ΔX1 < 0,即函數(1-1)為一條向右下傾斜的曲線;稱 | ΔX2 / ΔX1 | 為X1和X2的“邊際替代率”,如果要使總效用維持不變,則隨著某一商品消費量增加而必須放棄的另一商品的消費量將不斷減少,這就是所謂的“邊際替代率遞減規律”;這一規律說明,函數(1-1)為一條突向原點的曲線;在“序數效用論”中,這條體現同一效用水平、向右下傾斜並凸向原點的曲線被稱為“無差異曲線”;如果給定預算約束I = P1X1 + P2X2,必有一條無差異曲線與之相切,該切點即為效用最大化的均衡點;在切點處兩條曲線的斜率相等,因此有:
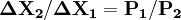 (1-2)
(1-2)
式(1-2)的意義在於,經濟學家似乎不用涉及效用的計量,只要通過消費變數ΔX和價格P,也可以推出與“基數效用論”同樣的結果,即一個理性的消費者將按照“效用最大化”的原則來決定他的行為。
在“序數效用論”中“無差異曲線凸向原點”是一個未經證明的假定,而“序數效用論”的其他結論、包括“邊際替代率遞減規律”和“切點定律”都是從這一前提中推導出來的。但通過分析不難發現,“無差異曲線凸向原點”與“邊際效用遞減”事實上是同一個假定,它們二者在邏輯上是完全等價的: 當效用水平U為一確定值U 0時,無差異曲線的方程可以表示為:
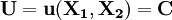 (C為一確定的常數) (2-1)
(C為一確定的常數) (2-1)
等式兩邊取全微分,有:
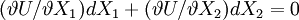 (2-2)
(2-2)
或:
 (2-3)
(2-3)
而
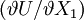 事實上就是X1 的邊際效用MU1,
事實上就是X1 的邊際效用MU1,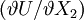 事實上就是X2的邊際效用MU2;如此則有:
事實上就是X2的邊際效用MU2;如此則有:
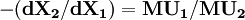 (2-4)
(2-4)
而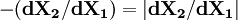 ,事實上就是X1和X2的“邊際替代率”,所以:
,事實上就是X1和X2的“邊際替代率”,所以:
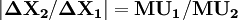 (2-5)
(2-5)
由式(2-5)我們可知,“無差異曲線凸向原點”和“邊際替代率遞減”完全是被“邊際效用遞減規律”所決定的,而“邊際效用遞減規律”則是建立在效用可以被計量即“基數效用論”的基礎上的。進一步,如果我們把式(2-5)代入前述式(1-5)則有:
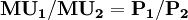
即: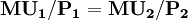 (2-6)
(2-6)
這樣一來,“序數效用論”用於描述效用最大化的均衡條件式就完全還原為“基數效用論”用於描述效用最大化的均衡條件式了。由此可見,“序數效用論”和“基數效用論”在邏輯上是完全等價的,








欠缺深入分析...