列昂惕夫逆矩陣
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
列昂惕夫逆矩陣又稱為完全需要繫數矩陣,其經濟意義是:增加某一部門單位最終需求時,需要國民經濟各個部門提供的生產額是多少,反映的是對各部門直接和間接的誘發效果。之所以稱為列昂惕夫逆矩陣,因為列昂惕夫是投入產出法的創始人。
列昂惕夫逆矩陣是指源於反映了直接效應引起的支出的乘數效應的交易表的矩陣。
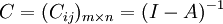
其中,A為直接消耗繫數矩陣。
列昂惕夫逆矩陣的元素 稱為列昂惕夫逆繫數。它表明第j個產品部門增加一個單位最終使用時,對第i個產品部門的完全需要量。
稱為列昂惕夫逆繫數。它表明第j個產品部門增加一個單位最終使用時,對第i個產品部門的完全需要量。
在傳統的競爭型投入產出表中,假設一個國家有n個部門,則由AX+Y=X可以推出X = (I − A) − 1Y,其中(I − A) − 1為列昂惕夫逆矩陣(AX+Y=X 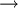 Y=(I-A)X
Y=(I-A)X 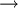 X = (I − A) − 1Y)。
X = (I − A) − 1Y)。
X = (I − A) − 1Y中的X是n*1l維總產出列向量,其中元素Xi代表i部門的總產出。A是n*n維直接消耗繫數矩陣,A中元素。J代表J部門生產1單位產品直接消耗i部門的產品量。Y是n*1維最終產品列向量,Y代表i部門的最終產品。將B = (I − A) − 1記做列昂惕夫逆矩陣,那麼B也是n*n維方陣,其中的元素bij代表部門j總產出增加1單位對部門i的完全消耗。
一些數學技術可以用來解投人一產出模型,而矩陣求逆是一個特別有用的方法,因為它產生了乘數。求逆方法從結構矩陣中產生了一種新的矩陣,即列昂惕夫逆矩陣。將列昂惕夫逆矩陣求和的一列就是產出乘數,反映了由直接(初始)效應引起的支出的倍數。由直接效應產生的額外的中間商品購買被稱為間接效應。額外的消費支出代表了誘發效應。直接、間接和誘發效應一起組成了經濟中一個變化的總效應。其他的測量收入和就業中變化的投人一產出乘數也可以算出來。








我是在研究全球價值鏈的時候看到的里昂惕夫矩陣,確實很有用