列昂惕夫逆矩阵
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
列昂惕夫逆矩阵又称为完全需要系数矩阵,其经济意义是:增加某一部门单位最终需求时,需要国民经济各个部门提供的生产额是多少,反映的是对各部门直接和间接的诱发效果。之所以称为列昂惕夫逆矩阵,因为列昂惕夫是投入产出法的创始人。
列昂惕夫逆矩阵是指源于反映了直接效应引起的支出的乘数效应的交易表的矩阵。
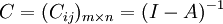
其中,A为直接消耗系数矩阵。
列昂惕夫逆矩阵的元素 称为列昂惕夫逆系数。它表明第j个产品部门增加一个单位最终使用时,对第i个产品部门的完全需要量。
称为列昂惕夫逆系数。它表明第j个产品部门增加一个单位最终使用时,对第i个产品部门的完全需要量。
在传统的竞争型投入产出表中,假设一个国家有n个部门,则由AX+Y=X可以推出X = (I − A) − 1Y,其中(I − A) − 1为列昂惕夫逆矩阵(AX+Y=X 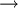 Y=(I-A)X
Y=(I-A)X 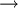 X = (I − A) − 1Y)。
X = (I − A) − 1Y)。
X = (I − A) − 1Y中的X是n*1l维总产出列向量,其中元素Xi代表i部门的总产出。A是n*n维直接消耗系数矩阵,A中元素。J代表J部门生产1单位产品直接消耗i部门的产品量。Y是n*1维最终产品列向量,Y代表i部门的最终产品。将B = (I − A) − 1记做列昂惕夫逆矩阵,那么B也是n*n维方阵,其中的元素bij代表部门j总产出增加1单位对部门i的完全消耗。
一些数学技术可以用来解投人一产出模型,而矩阵求逆是一个特别有用的方法,因为它产生了乘数。求逆方法从结构矩阵中产生了一种新的矩阵,即列昂惕夫逆矩阵。将列昂惕夫逆矩阵求和的一列就是产出乘数,反映了由直接(初始)效应引起的支出的倍数。由直接效应产生的额外的中间商品购买被称为间接效应。额外的消费支出代表了诱发效应。直接、间接和诱发效应一起组成了经济中一个变化的总效应。其他的测量收入和就业中变化的投人一产出乘数也可以算出来。








我是在研究全球价值链的时候看到的里昂惕夫矩阵,确实很有用