復相關係數

出自 MBA智库百科(https://wiki.mbalib.com/)

復相關係數(multiple correlation coefficient; coefficient of total correlation)

　　復相關係數是反映一個因變數與一組自變數(兩個或兩個以上)之間相關程度的指標。它是包含所有變數在內的相關係數。復相關係數是度量負相關程度的指標，它可利用單相關係數和偏相關係數求得。復相關係數越大，表明要素或變數之間的線性相關程度越密切。

　　復相關係數是測量一個變數與其他多個變數之間線性相關程度的指標。它不能直接測算，只能採取一定的方法進行間接測算。

　　為了測定一個變數y與其他多個變數X₁,X₂,...,X_k之間的相關係數，可以考慮構造一個關於X₁,X₂,...,X_k的線性組合，通過計算該線性組合與y之間的簡單相關係數作為變數y與X₁,X₂,...,X_k之間的復相關係數。具體計算過程如下：

　　第一步，用y對X₁,X₂,...,X_k作回歸，得：

　　第二步，計算y和 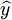的簡單相關係數，此簡單相關係數即為y與X₁,X₂,...,X_k之間的復相關係數。復相關係數的計算公式為：

　　之所以用R表示覆相關係數，是因為R的平方恰好就是線性回歸方程的決定繫數。這種關係的簡單推導如下：

　　在上面的式子中，分子可化為：

　　從而：

　　復相關係數與簡單相關係數的區別是簡單相關係數的取值範圍是[-1,1]，而復相關係數的取值範圍是[0,1]。這是因為，在兩個變數的情況下，回歸繫數有正負之分，所以在研究相關時，也有正相關和負相關之分；但在多個變數時，偏回歸繫數有兩個或兩個以上，其符號有正有負，不能按正負來區別，所以復相關係數也就只取正值。