複製性賣權策略
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄[隱藏] |
歐式保護性期權策略從理論上看似乎是無懈可擊,同時是簡便易行,但它有一個十分嚴格的隱含假設,即市場上存在有以風險資產組合S為標的資產的歐式看跌期權。另外該期權的期限與投資者的保險期一致。這實際上是很難做到的。因此,它的實際運用的可能性和有效性就大打折扣。Rubinstein &Leland(1981)設計出了複製性賣權,彌補了歐式賣權不足的地方,為OBPI 類投資組合保險開闢了新的領域。
複製性賣權策略的基本思想為,通過數學變換,將歐式保護性期權中的S和put的組合變為只有無風險資產和風險資產的組合,這樣一來,在理論上,投資者就毋須具有合適的協定價和期限的歐式看跌期權,而同樣可以達到歐式保護性期權策略對沖風險的目的。
具體數學模型如下所示:
V = S + P
其中S為風險資產組合,P為歐式賣權,V為組合保險。
由Black & Scholes(1973)推導出的無套利均衡的歐式看跌期權的定價模型:
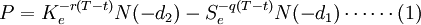
持有股票組合之投資者,若同時持有一保護性賣權,其含賣權之組合價值如下:
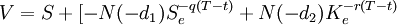
![=[1-N(-d_1)]S_e^{-q(T-t)}+N(-d_2)K_e^{-r(T-t)}](/w/images/math/b/6/9/b69aeac77fea2f16aeac7c231f02ede2.png)
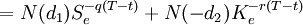
![=N(d_1)S_e^{-q(T-t)}+[ 1-N(d_2) ]K_e^{-r(T-t)}](/w/images/math/e/e/f/eefee3910ac29e5c144e1c7c98d34bbe.png)
由該式可看出受保組合之價值效果可由投資N(d1)百分比的現貨股票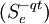 與1 − N(d2)的無風險債券
與1 − N(d2)的無風險債券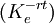 之組合來複制。例如投資者目前持有價格為S 之股票,欲將其價值在T 時保有不抵於K 之水平,此時它只要維持手中持股N(d1)的比例,而將1 − N(d1)比例之股票以當時價格出售,並將所得金額轉投於無風險債券。但隨著時間改變,S、t 的變動,會使得N(d1)也隨之變化,例如,當股價上漲時,d1值增加使得N(d1)也增加,投資者必須增持股票,亦即必須出售無風險資產,並以出售無風險資產所獲得的資金,供應增加持股之需;若遇股市下跌之際,則降低持股,並將出售股票所得轉投資於無風險資產,以符合自我融資(Self-financing)的特性。
之組合來複制。例如投資者目前持有價格為S 之股票,欲將其價值在T 時保有不抵於K 之水平,此時它只要維持手中持股N(d1)的比例,而將1 − N(d1)比例之股票以當時價格出售,並將所得金額轉投於無風險債券。但隨著時間改變,S、t 的變動,會使得N(d1)也隨之變化,例如,當股價上漲時,d1值增加使得N(d1)也增加,投資者必須增持股票,亦即必須出售無風險資產,並以出售無風險資產所獲得的資金,供應增加持股之需;若遇股市下跌之際,則降低持股,並將出售股票所得轉投資於無風險資產,以符合自我融資(Self-financing)的特性。

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 











