哈伯格三角形
出自 MBA智库百科(https://wiki.mbalib.com/)
哈伯格三角形(Harberger Triangle)
目錄 |
哈伯格三角形是運用補償需求曲線說明稅收超額負擔依據的是消費者剩餘理論。所謂消費者剩餘,就是指人們願意為某一種商品支付的金額和實際支付金額之差,它表示消費者從這一商品消費中獲得的凈收益。
哈伯格在《公司所得稅的歸宿》(1962年)中提出了“三角形”超額負擔理論,併進行數理推導,得出了線上性需求曲線條件下測定超額負擔的計算公式。
下圖顯示瞭如何運用補償需求曲線與消費者剩餘理論來說明稅收的超額負擔。
在上圖中,AB為某一產品的補償需求曲線。假設該產品的邊際成本為常數,稅前的邊際成本為MC,則稅前均衡價格為P0,產量為Q0,稅前消費者剩餘為AP0C。若政府對該產品征收從量稅T,則邊際成本曲線MC向上平易至MC’,此時均衡價格為PT,產量為QT,消費者剩餘為APTE。將稅前消費者剩餘與稅後消費者剩餘相比,稅收使消費者剩餘減少了PTECP0,,即稅收給消費者造成的福利損失。但政府收到的稅收收入僅為PTEDP0,,三角形ECD即為稅收的超額負擔。它是消費者失去的而政府又沒有得到的額外效率損失,因此又被稱為無謂損失。它完全是因為稅收改變了相對價格,消費者為了儘可能少納稅而改變了原有的有效選擇,從而導致的資源低效率配置所致。
理論上將三角形ECD稱為哈伯格三角形,通過計算這一三角形的面積即可計量稅收的超額負擔。計算公式為
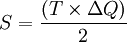
該公式中,T為單位產品的稅額,ΔQ為因價格變動而引起的需求量的變動額。如果用r來替代需求曲線的斜率 ,則上式可改寫為
,則上式可改寫為
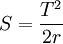









很好~