古典概率
出自 MBA智库百科(https://wiki.mbalib.com/)
古典概率(Classical Probability)
目錄 |
概率依其計算方法不同,可分為古典概率、試驗概率和主觀概率[1]。
人們最早研究概率是從擲硬幣、擲骰子和摸球等游戲和賭博中開始的。這類游戲有兩個共同特點:一是試驗的樣本空間(某一試驗全部可能結果的各元素組成的集合)有限,如擲硬幣有正反兩種結果,擲骰子有6種結果等;二是試驗中每個結果出現的可能性相同,如硬幣和骰子是均勻的前提下,擲硬幣出現正反的可能性各為1/2,擲骰子出出各種點數的可能性各為1/6,具有這兩個特點的隨機試驗稱為古典概型或等可能概型。計算古典概型概率的方法稱為概率的古典定義或古典概率。[1]
古典概率通常又叫事前概率,是指當隨機事件中各種可能發生的結果及其出現的次數都可以由演繹或外推法得知,而無需經過任何統計試驗即可計算各種可能發生結果的概率。[1]
關於古典概率是以這樣的假設為基礎的,即隨機現象所能發生的事件是有限的、互不相容的,而且每個基本事件發生的可能性相等。例如,拋擲一枚平正的硬幣,正面朝上與反面朝上是唯一可能出現的兩個基本事件,且互不相容。如果我們把出現正面的事件記為E,出現事件E的概率記為p(E),則:[2]
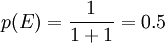 或
或
一般說來,如果在全部可能出現的基本事件範圍內構成事件A的基本事件有a個,不構成事件A的事件有b個,則出現事件A的概率為:[2]
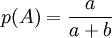
古典概率的基本特征[1]
1、可知性,可由演繹或外推法得知隨機事件所有可能發生的結果及其發生的次數。
2、無需試驗,即不必做統計試驗即可計算各種可能發生結果概率。
3、準確性,即按古典概率方法計算的概率是沒有誤差的。
古典概率的註意事項[2]
對毫無秩序的經營管理工作做出決策時,應用這種方法就會發生各種各樣的問題。這主要表現在:
1、古典概率的假想世界是不存在的。對於那些不能肯定發生,但又有可能發生的事情,古典概率不予考慮,如硬幣落地後恰恰站在它的棱上;一次課堂討論概率時突然著了火等。這些事情都是極其罕見的,但並非不可能發生,古典概率對這些情況一概不予考慮。
2、古典概率還假定周圍世界對事件的干擾是均勻的。這就是說,雖然按照古典概率的定義,拋平正的硬幣出現正面的概率等於0.5,但是誰敢打賭無論什麼時候拋10次準有5次出現正面呢?在實際生活中無次序的、靠不住的因素是經常存在的,為使概率具有使用價值,必須用其他方法定義概率。
古典概率舉例[1]
例如,同時擲兩枚硬幣,可能出現正正、反反、正反、反正四種可能的結果,每種可能出現概率1/4,如表1所示:
- 同時擲兩枚硬幣各種可能結果及概率
| 事件 | 可能結果 | 概率 |
|---|---|---|
| 1 2 2 3 4 | 正正 反反 正反 反正 | 0.25 0.25 0.25 0.25 |








有這種情況,這叫一次不成功的實驗,不能考慮它(因為他和兩外兩種情況不是等可能的),如果真的出現了處理方法有兩種1》不算數2》用力跺腳將其震倒