古典概率
出自 MBA智库百科(https://wiki.mbalib.com/)
古典概率(Classical Probability)
目录 |
概率依其计算方法不同,可分为古典概率、试验概率和主观概率[1]。
人们最早研究概率是从掷硬币、掷骰子和摸球等游戏和赌博中开始的。这类游戏有两个共同特点:一是试验的样本空间(某一试验全部可能结果的各元素组成的集合)有限,如掷硬币有正反两种结果,掷骰子有6种结果等;二是试验中每个结果出现的可能性相同,如硬币和骰子是均匀的前提下,掷硬币出现正反的可能性各为1/2,掷骰子出出各种点数的可能性各为1/6,具有这两个特点的随机试验称为古典概型或等可能概型。计算古典概型概率的方法称为概率的古典定义或古典概率。[1]
古典概率通常又叫事前概率,是指当随机事件中各种可能发生的结果及其出现的次数都可以由演绎或外推法得知,而无需经过任何统计试验即可计算各种可能发生结果的概率。[1]
关于古典概率是以这样的假设为基础的,即随机现象所能发生的事件是有限的、互不相容的,而且每个基本事件发生的可能性相等。例如,抛掷一枚平正的硬币,正面朝上与反面朝上是唯一可能出现的两个基本事件,且互不相容。如果我们把出现正面的事件记为E,出现事件E的概率记为p(E),则:[2]
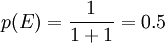 或
或
一般说来,如果在全部可能出现的基本事件范围内构成事件A的基本事件有a个,不构成事件A的事件有b个,则出现事件A的概率为:[2]
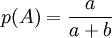
古典概率的基本特征[1]
1、可知性,可由演绎或外推法得知随机事件所有可能发生的结果及其发生的次数。
2、无需试验,即不必做统计试验即可计算各种可能发生结果概率。
3、准确性,即按古典概率方法计算的概率是没有误差的。
古典概率的注意事项[2]
对毫无秩序的经营管理工作做出决策时,应用这种方法就会发生各种各样的问题。这主要表现在:
1、古典概率的假想世界是不存在的。对于那些不能肯定发生,但又有可能发生的事情,古典概率不予考虑,如硬币落地后恰恰站在它的棱上;一次课堂讨论概率时突然着了火等。这些事情都是极其罕见的,但并非不可能发生,古典概率对这些情况一概不予考虑。
2、古典概率还假定周围世界对事件的干扰是均匀的。这就是说,虽然按照古典概率的定义,抛平正的硬币出现正面的概率等于0.5,但是谁敢打赌无论什么时候抛10次准有5次出现正面呢?在实际生活中无次序的、靠不住的因素是经常存在的,为使概率具有使用价值,必须用其他方法定义概率。
古典概率举例[1]
例如,同时掷两枚硬币,可能出现正正、反反、正反、反正四种可能的结果,每种可能出现概率1/4,如表1所示:
- 同时掷两枚硬币各种可能结果及概率
| 事件 | 可能结果 | 概率 |
|---|---|---|
| 1 2 2 3 4 | 正正 反反 正反 反正 | 0.25 0.25 0.25 0.25 |








有这种情况,这叫一次不成功的实验,不能考虑它(因为他和两外两种情况不是等可能的),如果真的出现了处理方法有两种1》不算数2》用力跺脚将其震倒