反應曲面法
出自 MBA智库百科(https://wiki.mbalib.com/)
反應曲面法(Response surface methodology; RSM)
目錄 |
反應曲面法是指為最適實驗設計或作業條件的有利工具結合數學與統計而延生出的方法。在1951年,Box和Wilson共同進行數學模式的建立與推導,而後普遍應用於電子、機械、農業、化學工業、生物科技、材料科學、食品科學及工業製程改善等各項研究領域中。
反應曲面法在協助研究人員對科學系統或工業製程中最佳產品設計、製程改善、系統優化等問題提供一套分析、求解程式,大部分應用時機均屬工業性研究,尤其是當系統特性受大量變數影響狀況下最為適當。
| 1920 | R.A.Fisher從基本的實驗設計技術的改進開始發展反應曲面法,並將農業及生命科學的實驗設計技術引進工業界。 |
| 1951 | Box和Wilson共同進行數學模式的建立與推導開始。 |
| 1966 | Hill和Hunter等相關研究下,其理論模式的建立與應用已趨於完整。 |
| 1966~1988 | 相關延伸的研究包含了探討模式的穩健性、可旋轉性、直交性、優化設計與自變數高度相關等因數實驗或混和實驗中常見問題,以及反應曲面法分析中之正規分析、脊線分析與雙反應曲面系統等。 |
| 1980 | 由於電腦模擬技巧應用於決策科學上漸受歡迎,反應曲面法亦成為分析複雜系統中重要影響變數的一項工具 |
| 2000至今 | 多反應值優化設計與多反應值共同優化問題成為反應曲面法研究的主流。 |
反應曲面法之研究問題,一般假設問題為限制性之優化問題,目標函數的確切型式是未知的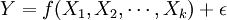 ,ε為誤差,反應曲面法一般在此前提的假設與應用系統的限制下,可有效地求得最佳實驗或作業變數值。
,ε為誤差,反應曲面法一般在此前提的假設與應用系統的限制下,可有效地求得最佳實驗或作業變數值。
一般來說,執行反應曲面法大致分為兩階段:
第一階段稱為反應曲面設計
第二階段稱為反應曲面優化
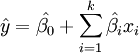
如果系統中有曲率,則必須利用較高階的多項式,如二階模型。
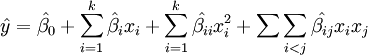
獲得最適化實務模型便是本階段最重要的議題。收集資料後以最小平方法配適,以尋找出一個適當近似的函數,採用回歸分析的顯著性檢定來瞭解獨立變數與反應變數間的關係強弱,並檢定配適的模式是否恰當。當實驗區域接近最佳反應值附近時,真實反應曲面的曲率會增加,則考慮二階模型,同樣的,我們需要檢定二階模式的適當性。當這個二階回歸模式配適良好時,便可以利用這二階模式求得最適操作點及特征化反應曲面。
| 反應曲面法是一個逐次的程式 。通常,當我們是在反應曲面的一個遠離最佳狀況的點時,系統只有少量的曲率而一階模型會是適當的,在此欲沿著改善路徑快速且有效地朝向最佳點(optimum)附近。 | |
進而利用最陡上升(下降)法。所配適一階模型的反應曲面,也就是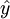 的等高線,沿著最大反應變數增加(減少)逐次移動程式,直到反應值無法再改善為止,其中,前進步伐的決定並非固定不變,可以根據實驗情況或經驗值決定,接著以此組操作水平為新的實驗中心點,並重覆實驗步驟,往最佳反應曲面的方向逼近,並且執行線性模式之缺適性檢定,一旦發現一階回歸模型不適合時,表示已接近最佳點,此時應採用更複雜的數學模式來進行分析。 的等高線,沿著最大反應變數增加(減少)逐次移動程式,直到反應值無法再改善為止,其中,前進步伐的決定並非固定不變,可以根據實驗情況或經驗值決定,接著以此組操作水平為新的實驗中心點,並重覆實驗步驟,往最佳反應曲面的方向逼近,並且執行線性模式之缺適性檢定,一旦發現一階回歸模型不適合時,表示已接近最佳點,此時應採用更複雜的數學模式來進行分析。 | 
|
| 如果選擇二階模式配適實驗數據時,一般進行中央合成設計實驗或是三水平因數設計,在配適及檢定二階模型完成之後,就進行反應曲面分析,指在目前實驗區域中,以實際不同情況(或製程限制)針對反應曲面系統作深入探討。此時可利用正規分析或脊線分析等技術來進一步瞭解穩定點之數學特性,其發現為鞍點則需進行更進一步的脊線分析,並配合反應曲面圖(或輪廓圖)的協助,若二階模式配適時仍存在缺適性之問題,則可以求得局部最佳操作狀態或再進而配適更高之回歸模式,如三次(cubic)或四次模型。 | 
|
經濟性原則:反應曲面法可以使用部分因數設計或特殊反應曲面設計(如混種設計等),以較少的實驗成本及時間獲得不錯且有效的信息。
深入探討因數間交互作用影響:反應曲面法可以經由分析與配適模式來研究因數間的交互作用,並且進而討論多因數對反應變數影響的程度。
獲得最適化的條件:根據數學理論求得最適的實驗情況,同時利用配適反應方程式繪出模式三度空間曲面圖與等高線圖,觀察並分析出最適的操作條件。
減少模擬時間:可獲得模擬獨立變數與反應變數關係之數學模型,藉此將實驗次數及時間降低。
在應用上主要存在下列二項限制:
只適用於連續性的系統,是假設所有反應值與獨立變數的量測刻度是連續性的。
影響系統之獨立變數(可控制和不可控制變數)是屬於計量性。







