效用曲線
出自 MBA智库百科(https://wiki.mbalib.com/)
效用曲線(utility curve)
目錄 |
效用曲線是用於反映決策者對風險態度的一種曲線。又稱"偏好曲線"。在決策中,決策者的個性、才智、膽識、經驗等主觀因素,使不同的決策者對相同的益損問題 (獲取收益或避免損失)作出不同的反應;即使是同一決策者,由於時間和條件等客觀因素不同,對相同的益損問題也會有不同的反應。決策者這種對於益損問題的獨特感受和取捨,稱之為“效用”。效用曲線就是用來反映決策後果的益損值對決策者的效用(即益損值與效用值)之間的關係曲線。通常以益損值為橫坐標,以效用值為縱坐標,把決策者對風險態度的變化在此坐標系中描點而擬合成一條曲線。
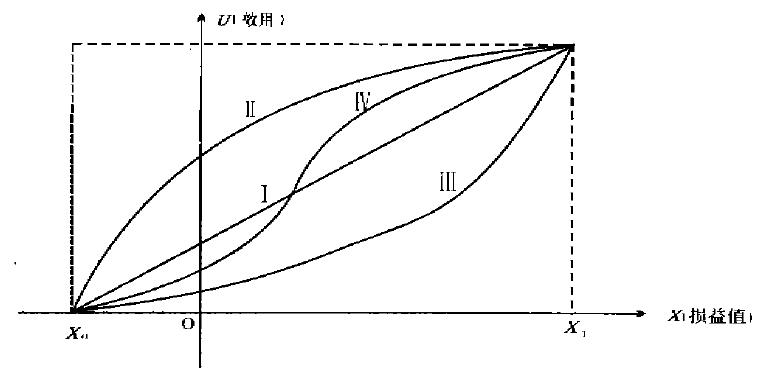
常見的效用曲線分為保守型、激進型、中間型和混合型四種, 見圖l。
圖1 效用曲線
1.保守型效用曲線
圖l中的曲線Ⅱ 嚴格上凸(下凹)表示效用隨著消費者收入的增多而遞增,但遞增速度越來越慢, 即邊際效用遞減,這樣的決策者對於虧損特別敏感,而大的收益對他的吸引力卻不是很大,這種類型的決策者容易滿足, 不求大利, 只求避風險。保守型決策者厭惡風險。
2.激進型效用曲線
圖l中的曲線Ⅲ是下凸(上凹)的,表示效用隨著消費者收入的增多而遞增, 而遞增速度越來越快, 即邊際效用遞增。曲線中間部分呈下凹形狀, 表示決策者專註於想獲得大的收益而不十分關心虧損,這種類型的決策者不易滿足。激進型決策者喜歡風險。
3.中問型效用曲線
圖l中的直線I表示決策的效用與決策損益的貨幣效果成線性關係, 對應於這種效用函數的決策者對決策風險抱中立態度,他或是認為決策的後果對大局無嚴重影響,或者因為該項決策可以重覆進行, 從而獲得平均意義上的成果, 因而對決策的某項後果不予特別關註,而謹慎從事,由於這類效用函數是線性美系,因此,效用期望值最大的方案也已是收益期望值的最大方案。此時一個非確定性決策的確定等價值就等於它的期望收益。
4.混合型效用曲線
圖1中的曲線Ⅳ 表示決策者在收 損益額不太大時,決策者具有一定的冒險膽略,追求風險屬於激進型,但當損益額增大到一定數量時,他就轉化為厭惡風險的決策者了,變為保守型, 其實這種類型更符合實際。
一般在一定的損益水平條件下,決策者認為效用越大,越傾向於保守型;反之決策者認為效用越小, 越傾向於風險型。
根據效用曲線的幾何特征可選用以下幾種統計學中常用的曲線來擬合效用曲線。圖1中的曲線Ⅱ 和Ⅲ 的擬合有多種形式.可以用Y = XO, 也可用半對數LnY=a+bX形式,以下採用指數函數形式。
1.直線——Y=A+BX
利用兩端點M(X1,1)和N(X0,0)確定直線I;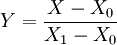 其中,y為效用參數,X為損益值(下同)。
其中,y為效用參數,X為損益值(下同)。
2.指數曲線—— 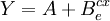
(1)曲線類型判斷。首先, 從繫數上判斷,從圖1可以看出曲線II和曲線III同為單調遞增函數,且曲線Ⅱ上凸, 曲線Ⅲ 下凹。
其次,利用期望效用直線判斷。當Ym > (Xm − X0) / (x1 − X0) 是,為保守型;
當Ym < (Xm − X0) / (X1 − X0)時,為激進型。
(2)模型求解。利用兩端點M(X1,1)和N(XO,0),決策損益效用點Q(Xm,Ym)滿足
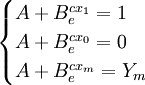 (1)
(1)
解得:
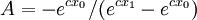 (2)
(2)
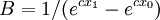 (3)
(3)
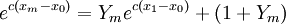 (4)
(4)
當曲線是保守型時, 設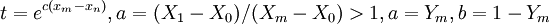 則(4)式可改寫成
則(4)式可改寫成
t = ata + b(0 < t < 1)
當曲線是激進型時, 設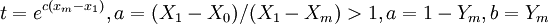 則(4)式也可改寫成(5)式。
則(4)式也可改寫成(5)式。
保守型: 由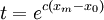 得C = lnt / (Xm − X0)
得C = lnt / (Xm − X0)
激進型: 由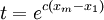
得C = Int / (Xm − X1),將C代人(2)式、(3)式,進而求出參數A,B。
3.混合型效用曲線
設效用函數是:
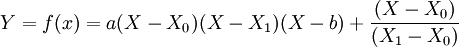
由Ym = f(Xm),Ym = f(Xn)解得:
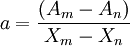 ,
,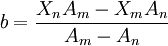
其中: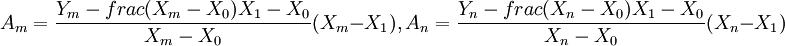
某決策者面臨三種建廠方案,決策矩陣如表1所示(單位: 萬元)。
表l
暢銷(0 7) 滯銷(0 3) 大廠 700 500 中廠 500 -300 小廠 300 —100
解: (1)極大損益效用點為M(700、1)'極小損益效用點為Ⅳ(一500~0).決策有損益效用點為;2(3O0,0.4)。
(2)判斷決策類型。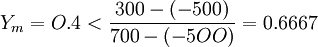 , 激進型。
, 激進型。
(3)模型求導解得: a=0.6,b=0.4,α=3,C=0.001955,A= -0.10588,B= 0.28l4, 即Y= -0.10588+ 0.2814e0.001955x。
(4)決策。將各行動方案不同狀態下損益值分別代人上式求出效用值, 然後計算出各行動方案的期望效用。
建大廠,U,== 0.7;建中廠,U =0.4646;建小廠,U =0.3177。
根據期望值極大原理, 應選擇建大廠方案, 如果決策者選擇損益效用點為Q(一200.0.49)可判斷為保守型, 利用上述方法,則應選擇建小廠方案。








問一下那個決策損益效用點是如何得出的啊?急用