二項期權定價模型
出自 MBA智库百科(https://wiki.mbalib.com/)
二項期權定價模型(Binomial options pricing model,SCRR Model,BOPM)
目錄 |
Black-Scholes期權定價模型雖然有許多優點, 但是它的推導過程難以為人們所接受。在1979年, 羅斯等人使用一種比較淺顯的方法設計出一種期權的定價模型, 稱為二項式模型(Binomial Model)或二叉樹法(Binomial tree)。
二項期權定價模型由約翰·考克斯(John Carrington Cox)、斯蒂芬·羅斯(Stephen A. Ross)、馬克·魯賓斯坦(Mark Rubinstein)和威廉·夏普(William F. Sharpe)等人提出的一種期權定價模型,主要用於計算美式期權的價值。
二項期權定價模型假設股價波動只有向上和向下兩個方向,且假設在整個考察期內,股價每次向上(或向下)波動的概率和幅度不變。模型將考察的存續期分為若幹階段,根據股價的歷史波動率模擬出正股在整個存續期內所有可能的發展路徑,並對每一路徑上的每一節點計算權證行權收益和用貼現法計算出的權證價格。對於美式權證,由於可以提前行權,每一節點上權證的理論價格應為權證行權收益和貼現計算出的權證價格兩者較大者。
1973年,布萊克和休爾斯(Blackand Scholes)提出了布萊克-休爾斯期權定價公式,對標的資產的價格服從正態分佈的期權進行定價。隨後,羅斯開始研究標的資產的價格服從非正態分佈的期權定價理論。1976年,約翰·考克斯(John Carrington Cox)、斯蒂芬·羅斯(Stephen A. Ross)在《金融經濟學雜誌》上發表論文“基於另類隨機過程的期權定價”,提出了風險中性定價理論。
1979年,約翰·考克斯(John Carrington Cox)、斯蒂芬·羅斯(Stephen A. Ross)、馬克·魯賓斯坦(Mark Rubinstein)在《金融經濟學雜誌》上發表論文“期權定價:一種簡單的方法”,該文提出了一種簡單的對離散時間的期權的定價方法,被稱為Cox-Ross-Rubinstein二項式期權定價模型。
二項式期權定價模型和布萊克-休爾斯期權定價模型,是兩種相互補充的方法。二項式期權定價模型推導比較簡單,更適合說明期權定價的基本概念。二項式期權定價模型建立在一個基本假設基礎上,即在給定的時間間隔內,證券的價格運動有兩個可能的方向:上漲或者下跌。雖然這一假設非常簡單,但由於可以把一個給定的時間段細分為更小的時間單位,因而二項式期權定價模型適用於處理更為複雜的期權。
隨著要考慮的價格變動數目的增加,二項式期權定價模型的分佈函數就越來越趨向於正態分佈,二項式期權定價模型和布萊克-休爾斯期權定價模型相一致。二項式期權定價模型的優點,是簡化了期權定價的計算並增加了直觀性,因此現在已成為全世界各大證券交易所的主要定價標準之一。
一般來說,二項期權定價模型的基本假設是在每一時期股價的變動方向只有兩個,即上升或下降。BOPM的定價依據是在期權在第一次買進時,能建立起一個零風險套頭交易,或者說可以使用一個證券組合來模擬期權的價值,該證券組合在沒有套利機會時應等於買權的價 格;反之,如果存在套利機會,投資者則可以買兩種產品種價格便宜者,賣出價格較高者,從而獲得無風險收益,當然這種套利機會只會在極短的時間里存在。這一 證券組合的主要功能是給出了買權的定價方法。與期貨不同的是,期貨的套頭交易一旦建立就不用改變,而期權的套頭交易則需不斷調整,直至期權到期。
二項樹期權定價模型的應用非常廣泛,因為它能夠在很多情況下使用,而其他模型往往只能針對特定的情況。廣泛的應用性是因為二項樹期權定價模型基於標的資產在一段時間內的變化,而非一個時間點的價格。因此,二項樹期權定價模型可以用於可在任意時間行權的美式期權的定價,也可應用於可在一系列特定時間行權的百慕大期權的定價。因為它的簡單性,二項樹期權定價模型已經被內置於眾多軟體中。
雖然計算要慢於布萊克-舒爾斯-墨頓模型(BSM Model),但是二項樹期權定價模型更加準確,特別是應用於時間長且會有分紅的股票期權。
應用:
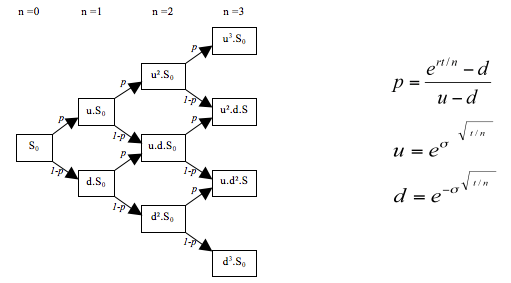
第一步:創建價格二項樹
價格二項樹的創建由估值日向期權到期日一步一步向前推。
在每一步,假設標的資產價格都會移動u或者d(u>=1, 0<d<=1)。所以,如果S是當前價格,那麼在下一步,價格會變成Su=S*u,或者Sd=S*d。價格移動的幅度取決於標的資產價格的波動率σ,和每一步的以年表示的時間長度t。
u=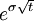
d=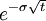 =
=
如果標的資產價格向上移動u,再向下移動d, 那麼價格又回到了移動之前。這個特性讓每個節點的資產價格能通過簡單的公式計算出來,而不需要首先構建價格二項樹。
Sn=S0×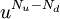
其中 Nu是價格向上運行的次數,Nd是價格向下運動的次數。
第二步:找出每個最終節點上的期權價值
在二項樹的每一個最終節點上,即期權的到期日,期權的價格為它的內在價值,也就是執行價值。
對於認購期權:Max [ (Sn-K), 0 ]
對於認沽期權:Max [ ( K–Sn ), 0 ]
其中
K是期權的行權價格;
Sn是標的資產在第n
第三步:找出更早節點上期權的價值
1)在風險中性假設下,今天一個衍生品的公允價格等於它以無風險利率來折現的未來收益的期望價值。因此,期望價值的可由之後的兩個節點計算得出,分別給價格向上運動賦予概率p,給價格向下運動的賦予概率(1-p)。
期權價值 = [ p × Option up + (1-p) × Option down] × exp (- r × Δt)
或者
其中
Ct,i是第ith個節點在時間t的價值;
p=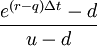 是標的資產價格向上運動的概率;
是標的資產價格向上運動的概率;
q 是標的資產在期權到期前的股息收益率。
1)根據此方法,求出來的即為二項樹價值。它代表了給定價格變化的情況下,期權在特點時點的公允價值。
2)根據期權類型的不同,判斷每一個節點上期權提前執行的概率:如果期權能夠執行,且行權價值高於二項樹價值;那麼節點價值為行權價值。
對於歐式期權,期權不能提前執行,二項樹價值可應用於所有節點。
對於美式期權,因為期權可以持有,也可在到期日前行權,所以在每個節點上,期權價值為Max(二項樹價值,行權價值)。
評論(共16條)
構造無套利均衡模型來推還比較容易理解的
你理解了?麻煩給我解釋下,好嗎?
麻煩把最後幾步推導過程寫出來吧,還是理解不透!
添加了文獻出處,希望對您有幫助!~
太不清楚了 公式編輯混亂
做了修改,希望對大家有幫助!
如果沒看錯的話,英文應該是Binomial Option Pricing Model...澳洲學渣路過。。。
謝謝指正,已修改!








“或者說可以使用一個證券組合來模擬期權的價值,該證券組合在沒有套利機會時應等於買權的價 格;”————不知這樣說是否有點問題,是否相當是說,“你怕權證的成本回不來了吧,好,那你想零損失,就先假設會發生損失,現在就再投其他的錢預備能賺相同的錢回來以彌補這損失”,難道這種邏輯沒有問題嗎?