久期匹配模型
出自 MBA智库百科(https://wiki.mbalib.com/)
久期匹配模型(Duration Matching)
目錄 |
如果給定了一組現金流量,某種證券的久期可以計算出來,從概念上看,久期可以看成是現金流量的時間加權現值。久期匹配(或稱免疫)法就是要在資產組合中將資產與負債的利率風險相匹配。該方法傳統的模型假定利率期限結構平緩且平行變動。
當然目前很多模型得到了擴展,用以管理利率期限結構曲線形狀變動等引起的現金流量的波動風險、流動性風險及信用風險。由於久期隨利率波動而變化,即使最初資產與負債的久期是匹配的,隨著利率的變化它們的久期就可能不再匹配,為此提出了一個“有效久期”概念。有效久期依賴於資產價格相對於利率變化的變動率,這個變動率由其凸性衡量。也就是說,金融機構為確保資產負債的匹配,不僅要求資產負債的久期匹配,而且通過控制資產和負債的凸性,通過資產和負債的久期和凸性的匹配,來更精確地規避風險。
免疫模型有很多種,最常見是將資產組合的收益作為目標函數。我們以其中一種模型為例 ,用數學公式表示如下:
模型:目標: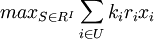
限制: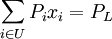
其中:
- U = {1,2,3,…I}為證券集;
- T = {1,2,3,…Tmax} 為不連續的時間點集;
- xi:證券i的持有量;
- ri:現金流量收益;
- Pi:證券i的現值;
- ki:證券i的久期。
由模型的假設可以看出,久期匹配模型適用於固定收益的資產負債管理。即使是這樣,久期匹配的資產與負債能否真正免疫也值得懷疑。如果把價格視為必要收益率的函數,則久期及凸性分別直接依賴於其一階導數與二階導數。人們作了很多研究,試圖確定重新平衡資產組合以達到指定久期的動態資產組合是否能夠有效免疫。其中一篇利用隨機過程的研究報告似乎證實免疫確實能夠有效規避風險,但這份研究報告又指出,如此滿意的結果是基於“市場有效及對利率變化過程的描述是正確的”這樣一種聯合假設基礎上的,對於違背這個聯合假設的其他情況,報告結論是“也許並不能免疫”。可以看出,用隨機模擬方法或稱為“Lattice construction(格子構造)”的方法得出的免疫策略的成功,對於真正的資產負債管理的全過程並不穩健,或者說其實際用途值得懷疑,這種方法的成功或許只能說明,用複雜的數學模擬技術做點理論研究是有益的,它可探討任意複雜的隨機結構。







