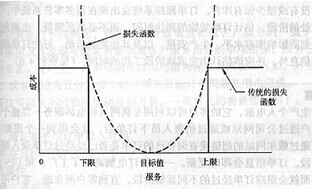
损失函数

出自 MBA智库百科(https://wiki.mbalib.com/)

损失函数（Loss Function）

　　损失函数（loss function）或代价函数（cost function）是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。例如在统计学和机器学习中被用于模型的参数估计（parametric estimation） ，在宏观经济学中被用于风险管理（risk management）和决策 ，在控制理论中被应用于最优控制理论（optimal control theory）。

　　损失函数是指一种将一个事件（在一个样本空间中的一个元素）映射到一个表达与其事件相关的经济成本或机会成本的实数上的一种函数,较常运用在统计学，统计决策理论和经济学中。损失函数参数的真值为（θ），决策的结果为d ，两者的不一致会带来一定的损失，这种损失是一个随机变量，用L(θ,d)表示。

　　常见的损失函数有L(θ,d) = c(θ − d)²(称为二次损失函数）和L(θ,d) = c | θ − d | （称为绝对损失函数）。

　　损失函数是描述系统在不同参数（parameter）值之下的损失。要应用损失的函数，其损失必须是通过某种媒介可以衡量的。

　　损失函数在实践中最重要的运用，在于协助我们通过过程的改善而持续减少目标值的变异，并非仅仅追求符合逻辑。

　　现在举个例子：某个工厂人员的产出，以每小时多少元来计算，而损失函数所显示的，是产出以室内通风条件而改变的情形。厂内工作的每个人，都有自己的损失函数。为了简化说明，假设每个人的损失函数均为一条抛物线，其底部一点代表产出值最大时的通风条件，把所有人员的损失函数进行叠加，公司整体的损失函数也必然是一条抛物线。如果通风条件偏离这个最佳水准，就会有额外损失发生。当该抛物线与横轴相切时，切点的左右各有一小段与横轴几近重合。也就是说，由最适点偏离一小短距离，损失小到可以忽略不计。因此，当室内通风条件稍稍偏离均衡点，发生的损失可以忽略不计。但是远离均衡点时，总是有人必须支付这损失。如果我们能够导出有具体数字的损失函数，我们就可以计算出最优均衡点，在均衡点中最适合的通风条件如何，以及达到要求的费用支出是多少。

　　随着服务偏离目标值，损失会递增。递增速度如下：

　　L=k(y-m)²

　　L——以美元表示的单位损失（惩罚成本）

　　y——质量变量的值

　　m——质量变量y的目标值

　　k——常数，取决于质量变量在财务上的重要性。

　　某匹萨外卖店承诺在接到订单30分钟内送货。如果超过承诺时间10分钟，那么将赔偿金额3美元。送货成本大概是2美元，但是，随着送货时间的推迟，送货成本将以0.15美元/分钟的速度下降。实际送货时间应偏离目标送货时间多长，能使成本最低？

　　总成本（N）=送货成本（J）+赔偿成本（L）

　　设实际送货时间为y

　　送货成本J=2-0.15（y-30）

　　赔偿成本L=k(y-30)²

　　N=L+J=k(y-30)²+[2-0.15(y-30)]

　　首先求出k,再求出Min(N)。如何求k?

　　L=k(y-30)²

　　3=k(10-0)²

　　Min(N)=Min{0.03(y-30）²+[2-0.15(y-30)]}

　　求导，得出y-30=2.5,即实际送货时间不偏离目标时间2.5分钟以上。

• 风险函数