最优一篮子货币

出自 MBA智库百科(https://wiki.mbalib.com/)

　　篮子货币的最优权重都是由特定的政策目标所决定，不同政策目标下所得到的篮子货币的最优权重是不同的。各种模型在求解货币篮子最优权重的过程中，都是首先确定研究对象国选择一篮子货币汇率制度的政策目标，建立一定的政策目标函数，然后才能去求解货币篮子的最优权重。

　　确定最优一篮子货币有两种方法：

　　一是局部均衡分析法。即将汇率看作外生变量，只考虑商品流动而忽略资本流动，计算的最优货币权重通常与本国出口量、本国进口量，本国对一国的出口占本国出口总额的比重，本国从一国的进口占本国进口总额的比重，本国出口供给弹性和本国进口需求弹性以及本国的出口竞争力和进口竞争力有关。局部分析法的追求目标包括稳定有效汇率，稳定实际国民收入增长，稳定贸易余额，稳定贸易条件的稳定或贸易品与非贸易品相对价格，稳定外债真实价值。由于局部均衡分析法对数据要求具有灵活性，因此，在确定最优一篮子货币时成为主流研究方法。

　　二是一般均衡分析法。Flanders和Helpman的宏观经济模型中，将国际收支的稳定视为一篮子货币制度的追求目标，同时考虑了本国出口需求和本国进口需求量、贸易量对本币汇率变化的弹性、就业水平和贸易条件等一系列变量之间的相互影响。Turnovsky的宏观经济模型中，国际贸易方面的因素对最优一篮子货币的权重结构不具有决定性作用，本币与外币之间的双边汇率波动、两国通货膨胀率和利率水平的变动、以及反映经济特征的结构性因素都成为决定最优一篮子货币的关键变量。Bird和Rajan则将物价稳定和充分就业作为一篮子货币制度的政策目标，兼顾一国的外债结构，根据一国国际贸易状况、外债币种结构和两国物价水平差异确定了最优一篮子货币的三个决定要素。一般均衡分析法往往需要设定复杂的经济主体行为特征函数和各经济变量之间多样的关系方程，要求的数据量和计算大大高于局部均衡分析法，所以尚未成为一篮子货币学术研究的主流研究方法。

　　根据Frankel和Wei的对数线性模型：

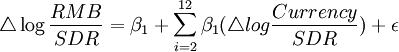　　　　(1)

　　其中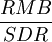，表示SDR计价的人民币汇率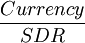，表示SDR计价的第i种货币，i从1到11，分别表示美元、欧元、日元、英镑、韩元、泰铢、马来西亚林吉特、俄罗斯卢布、新加坡元、澳元、加元。方程系数β₁表示截距，i=2，…12，可以解释为一篮子货币中11种货币的权重，对从2005年8月到2009年4月(45个观察值)人民币与11种货币之间的关系进行线性对数回归，并用SPSS7.0的后退剔除法进行多重共线性检验，依次剔除了新元、加元、俄罗斯卢布、泰铢和马来西亚林吉特，最后得到以美元、英镑、日元、韩元、欧元、澳元六种货币为解释变量的回归方程，表明人民币货币篮子里这六种货币对人民币的影响是显著的。

　　Williamson认为，最优货币篮子的权重应当由贸易决定，这样可以保持有效汇率的稳定，使主要货币汇率的随机变化对一国实体经济的冲击影响减少，同时保持宏观经济的健康发展，以及贸易品相对价格和产出的稳定。

　　若中国有n个贸易伙伴国，与第i国贸易额用T_i表示，则中国贸易总额为：

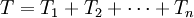　　　　(2)

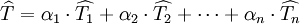　　且有：　　(3)

　　。

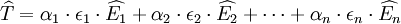　　根据Branson和Katseli，一国政策目标应当是追求稳定就业。假设一国产业结构中贸易占重要地位，则稳定就业就意味着稳定贸易额，即最优一篮子货币的权重()，使得贸易额变动最小化：

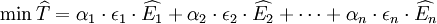
　　subjece to:

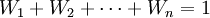
　　经过推导可得最优权重：

　　……

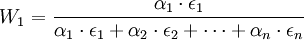
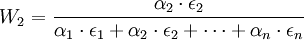
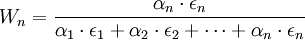
　　因此，一国的最优货币篮子取决于一国贸易伙伴的汇率弹性与对该伙伴国贸易最占份额。如果各贸易伙伴国弹性ε₁相等，则最优货币篮子的权重完全由一国与贸易伙伴国的贸易份额决定。

• 一篮子货币
• 参考一篮子货币
• 盯住一篮子货币