整群抽样
出自 MBA智库百科(https://wiki.mbalib.com/)
整群抽样 (Cluster sampling)
目录 |
整群抽样又称聚类抽样。是将总体中各单位归并成若干个互不交叉、互不重复的集合,称之为群;然后以群为抽样单位抽取样本的一种抽样方式。
应用整群抽样时,要求各群有较好的代表性,即群内各单位的差异要大,群间差异要小。
整群抽样的优点是实施方便、节省经费;
整群抽样的缺点是往往由于不同群之间的差异较大,由此而引起的抽样误差往往大于简单随机抽样。
| 市场调查方法 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [编辑] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
先将总体分为i个群,然后从i个群中随机抽取若干个群,对这些群内所有的或部分选中的个体或单元均进行调查。抽样过程可分为以下几个步骤:
一、确定分群的标准。
二、总体(N)分成若干个互不重叠的部分,每个部分为一群。
三、据各样本量,确定应该抽取的群数。
四、采用简单随机抽样或系统抽样方法,从i群中抽取确定数量的个体或单元。
整群抽样的误差[1]
整群抽样的误差视各群单位方差大小而定,各群单位方差的简单平均数是计算其抽样平均误差的依据。从公式上看,整群抽样平均误差的公式与类型抽样平均误差的公式相似,用R表示全及总体中划分的群(组)数。r表示被抽中的群(组)数。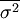 表示抽样总体各群(组)方差的平均数。
表示抽样总体各群(组)方差的平均数。
整群抽样平均数的抽样平均误差为:
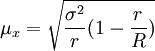
成数的抽样平均误差为:
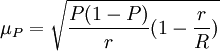
整群抽样与分层抽样在形式上有相似之处,但实际上差别很大。
分层抽样要求各层之间的差异很大,层内个体或单元差异小,而整群抽样要求群与群之间的差异比较小,群内个体或单元差异大;
分层抽样的样本时从每个层内抽取若干单元或个体构成,而整群抽样则是要么整群抽取,要么整群不被抽取。
分层抽样与整群抽样对比
1.分层抽样
某公司的雇员按照部门(销售部、市场部、研究部、广告部)分层,在每一个部门随机抽取10名雇员。
2.整群抽样
福尔摩斯特旅馆连锁店有10家酒店,从中随机地选取5家,对被选出的每家酒店的全部雇员进行调查。
案例一:整群抽样在平原绿化调查中的应用[2]
平原绿化调查一般是指针对一个县或几个县的较大范围内进行调查,调查内容比较多,范围广,困难大。以往采用的公里网机械布点调查方法,在调查时,布点工作量大,时间长,操作很不方便。近几年在村镇绿化率及农田林网化调查时,我们采用了整群抽样法进行调查,取得了很好的效果,大大减轻了布点工作量,并且其调查统计中的各个特征数完全能够达到预定的要求。我们认为,这种抽样方法可以在平原绿化调查或其他较大范围的林业调查中推广应用。
一、整群抽样技术简介
整群抽样是将全部总体单元划分为若干部分,把划分的每一部分称为一个“群”,然后抽取若干个“群”,对这些“群”进行调查,估计总体。
在将全部总体单元划分为若干群时,有下列要求:第一,群与群之间无重叠,即任何一个总体单元只属于某一个群;第二,全部总体单元毫无遗漏,即任何一个总体单元必定属于某一个群;第三,每一个群包含的单元数可以是相同的,也可以是不相同的,但必须是确知的。
在对群进行抽样,以组成样本时,可以采取等概方式,也可以采取不等概方式;可以采取重复抽样方式,也可以采取不重复抽样方式。
用整群抽样法对总体进行估计时,根据每个群内包含的总体单元数是否相等,分等群估计和不等群估计两种方法。
二、整群抽样法的应用
在陵县、临邑两县村庄绿化率调查的方法介绍如下:
1.划分群体、抽样
两县村庄占地面积共2.6万h㎡ ,将667㎡土地作为一个总体单元,即有39万个总体单元,这些总体单元分布在2165个村中。根据总体划分群的要求,我们可以将村做为群,则两个县共有2165个群。每群所包括的单元数为各村的占地面积数。
由于每个村面积不等,即每个群的单元数是不相等的,所以我们划分的群是不等群,在进行总体估计时,用不等群估计方法。
抽取样本的个数,应根据总体的变动系数来确定。这里,我们预计变动系数时,用下面方法进行计算:根据档案材料,查找出两个县前一年的统计报表,在报表中随机抽出50 个村的林木覆盖数字,以此做为样本,求出其标准差和平均数,由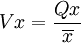 求得变动系数为0.41 ,这个数字可做为总体的估计变动系数。
求得变动系数为0.41 ,这个数字可做为总体的估计变动系数。
根据估计的变动系数及95 %的可靠性(ua=1.96) 和90%的精度(P) 要求, 由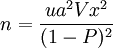 求得样本个数为:
求得样本个数为: 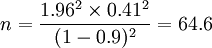 取整数为65 。
取整数为65 。
在总体所有的群中,用简单随机抽样法等概地抽取65 个群组成样本,对总体进行估计。
2.样群调查
对抽中的村庄四旁树木进行逐棵查数,每隔10株测算一棵树冠投影面积,以算术平均法求得每株平均投影面积,再乘以总株数得林木覆盖面积。
通过全面调查,获得65个样群的调查资料,调查数据按样群编号1 ,2 ,3 ……65列出, ( 省略村名) 。见下表
表 65个样群调查数据
| 样群号i | 林木覆盖面积yi | 样群号i | 林木覆盖面积yi | 样群号i | 林木覆盖面积yi |
| 1 | 96 | 23 | 95 | 45 | 43 |
| 2 | 49 | 24 | 72 | 46 | 114 |
| 3 | 71 | 25 | 43 | 47 | 92 |
| 4 | 29 | 26 | 88 | 48 | 95 |
| 5 | 58 | 27 | 36 | 49 | 109 |
| 6 | 31 | 28 | 36 | 50 | 121 |
| 7 | 82 | 29 | 74 | 51 | 130 |
| 8 | 44 | 30 | 52 | 52 | 72 |
| 9 | 88 | 31 | 63 | 53 | 90 |
| 10 | 65 | 32 | 44 | 54 | 57 |
| 11 | 56 | 33 | 60 | 55 | 37 |
| 12 | 38 | 34 | 35 | 56 | 33 |
| 13 | 78 | 35 | 62 | 57 | 40 |
| 14 | 85 | 36 | 40 | 58 | 53 |
| 15 | 58 | 37 | 67 | 59 | 26 |
| 16 | 83 | 38 | 43 | 60 | 50 |
| 17 | 40 | 39 | 72 | 61 | 59 |
| 18 | 60 | 40 | 82 | 62 | 72 |
| 19 | 62 | 41 | 67 | 63 | 57 |
| 20 | 52 | 42 | 74 | 64 | 54 |
| 21 | 39 | 43 | 27 | 65 | 53 |
| 22 | 77 | 44 | 49 | Σyi | 4037 |
3.计算
因为调查的村庄林木覆盖率为频率范围,因而采用总体频率的不等群估计方法。
村庄林木覆盖率(总体频率) 整群抽样估计值为:
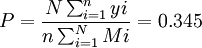 即34.5%
即34.5%
估计误差限为:
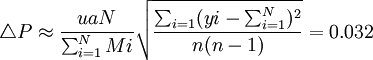
总体频率P的置信区为[P-ΔP,P+ΔP]即[31.3%,37.7%]。如果计算精度,则估计精度为1-ΔP/P=90.7%。式中:P为总体频率,N为总体内全部群数,n为样本群数,yi为具备某特征单元数,Mi为每群单元数。
三、使用整群抽样应注意的几个问题
1.只有在总体单元数非常大,群数相当多时,才能用整群抽样进行估计取得整群抽样的估计效率。
2.只有总体中N 群的Yi具有正态(近似正态) 的频率分布时,才可采用小样本估计方法。
3.划分的各群内单元数相同的,采用整群抽样的等群估计方法,其主要公式为:
(1) 总体平均数估计值:样群误差限:
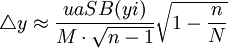
其中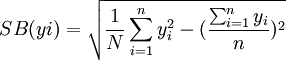
(2) 总体频率的估计值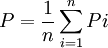
估计误差限: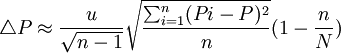
式中:y 为样本平均数: P为样本频率;yi、Pi为样本标志值; n为样本个数;M为一个群所含的单元数;SB(yi) 为标准差。








如果有案例就好了!