干预分析模型预测法
出自 MBA智库百科(https://wiki.mbalib.com/)
干预分析模型(Intervention analysis model)
目录 |
①干预的含义:时间序列经常会受到特殊事件及态势的影响,称这类外部事件为干预。是指预测模型拟合的好坏程度,即由预测模型所产生的模拟值与 历史实际值拟合程度的优劣。
②研究干预分析的目的:从定量分析的角度来评估政策干预或突发事件对经济环境和经济过程的具体影响。
干预分析模型的基本变量是干预变量,有两种常见的干预变量:一种是持续性的干预变量,表示T 时刻发生以后, 一直有影响,这时可以用阶跃函数表示,形式是:
第二种是短暂性的干预变量,表示在某时刻发生, 仅对该时刻有影响, 用单位脉冲函数表示,形式是:
干预事件虽然多种多样,但按其影响的形式,归纳起来基本上有四种类型:
- a. 干预事件的影响突然开始,长期持续下去,设干预对因变量的影响是固定的,从某一时刻T开始,但影响的程度是未知的,即因变量的大小是未知的。
这种影响的干预模型可写为
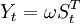
表示干预影响强度的未知参数。 不平稳时可以通过差分化为平稳序列,则干预模型可调整为
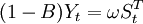
其中B为后移算子。如果干预事件要滞后若干个时期才产生影响,如b个时期,那么干预模型可进一步调整为
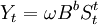
- b. 干预事件的影响逐渐开始,长期持续下去有时候干预事件突然发生,并不能立刻产生完全的影响,而是随着时间的推移,逐渐地感到这种影响的存在。
这种形式的最简单情形的模型方程为
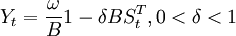
更一般的模型是:
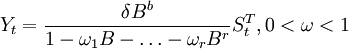
- c. 干预事件突然开始产生暂时的影响,这类干预现象可以用数学模型描述如下:
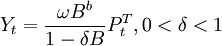
当δ = 0时,干预的影响只存在一个时期,当δ = 1时,干预的影响将长期存在。
- d. 干预事件逐渐开始产生暂时的影响
干预的影响逐渐增加,在某个时刻到达高峰,然后又逐渐减弱以至消失。这类干预现象可用以下模型去描绘:
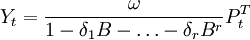
- (1)干预模型的构造与干预效应的识别
单变量时间序列的干预模型,就是在时间序列模型中加进各种干预变量的影响。设平稳化后的单变量序列满足下述模型:
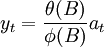
又设干预事件的影响为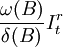 ,其中
,其中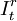 为干预变量,它等于
为干预变量,它等于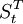 或
或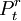 ,则单变量序列的干预模型为
,则单变量序列的干预模型为
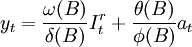

这里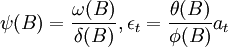
在此模型基础上要根据序列变化的现实资料,对ψ(B)与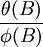 进行识别。
进行识别。
干预模型建模的思路和具体步骤为:
a.利用干预影响产生前的数据,建立一个单变量的时间序列模型。然后利用此模型进行外推预测,得到的预测值,作为不受干预影响的数值。最后将实际值减去预测值,得到的是受干预影响的具体结果,利用这些结果可以求估干预模型的参数。
b.估计出干预模型的参数。
c.利用排除干预影响后的全部数据,识别与估计出一个单变量的时间序列模型。
d.求出总的干预分析模型。
案例一:中国钢铁产品市场价格干预分析模型研究[1]
一、引言
钢铁产品市场价格的变化受多种因素的影响,这种影响是随机的均衡的。但现实生活中这些因素有时是突变的,对钢材市场造成冲击和干预,尤其是宏观经济政策、政治自然等因素。如何将这种影响的幅度和持续性定量地描述出来,对于深入认识我国钢材市场的波动特征是非常有意义的。
二、宏观调控及对钢材市场的影响
2005年中国钢材市场在大起大落中走过了极不平静的一年。自2004年12月中旬国内钢材市场开始呈现出“淡季不淡”,价格“逆市”上扬的运行态势后,在2005年初更是借助铁矿石进口协议价格大幅上涨“东风”的推动,价格持续大幅走高,使得市场风险明显走高,加之市场需求的跟进乏力,部分商家信心也开始有所动摇。3月30日温家宝总理主持召开国务院常务委员会,会议强调要加强对钢铁行业、房地产行业的宏观调控,此后一系列针对钢铁和房地产行业的调控措施陆续出台,从3月下旬起,国内钢材市场开始进入了漫长的下行通道。
2005年的宏观调控明显具有针对性。2004年国家通过提高央行准备金率、清理固定资产投资项目、清理整顿开发区等方式给所有投资降温。2005年的目标则定位明确,针对钢材价格上涨过快的问题,国家集中出台了一系列宏观调控措施抑制钢材价格,这些措施既有针对钢铁行业本身的,也有针对下游消费行业的。从2005年4月1日起正式取消钢坯、钢锭出口退税;从2005年5月1日起将2O种钢材产品的出口退税率从13%下调至11%;从2005年5月19t3起将铁矿石、生铁、废钢、钢坯等产品列入加工贸易禁止类商品目录,这是对钢铁行业本身的调控措施;2005年3月29日,国土资源部提出今年将继续严格土地市场治理整顿,继续实行从严从紧的建设用地供应政策,严把土地闸门;国务院办公厅2005年5月11日转发建设部等七部委《关于做好稳定住房价格工作的意见》,通知要求要解决房地产投资规模过大、价格上涨幅度过快等问题,这是对钢材消费行业采取的调控措施。
这些政策传递了中央通过控制需求,进而控制重要生产资料价格过快上涨的决心。这一系列措施抑制了钢材需求增长,导致钢材库存增加,企业流动资金困难,引发了包括板材在内的国内钢材市场价格大幅下滑。宏观调控对人的心理预期很大,钢铁企业、下游厂商和经销商普遍预期钢材价格下跌,导致推迟电货,这就肯定会影响需求。
政府宏观调控政策的紧密出台打压了钢材市场的中间需求和有效需求的释放,促使钢材市场出现下跌。一方面国内的贸易商心态变差,为了缓解紧张的资金压力及保住市场份额,纷纷降价;另一方面影响了市场有效需求的释放,尽管国内钢材市场真实需求依旧相对坚挺,但受消费用户买涨不买跌心理影响,市场有效需求释放不足,观望气氛浓厚。
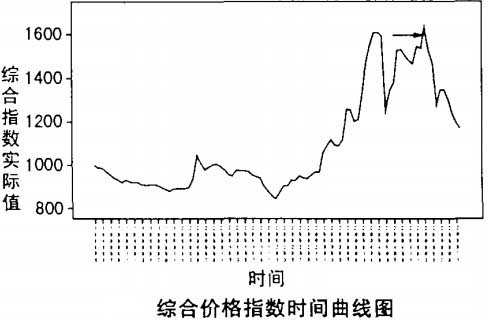
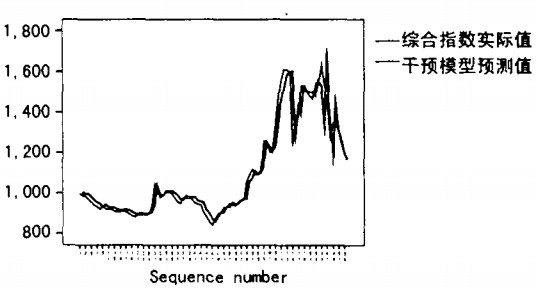
从以上分析可以看出,2005年4月是钢材市场的一个分水岭,其中宏观经济政策干预效用明显。下图是1998年3月至2005年12月中国钢材市场综合价格指数时间曲线图(采样频率一月一次),箭头所示为2005年4月市场价格峰值。(见下图)。
三、干预分析模型的理论
干预分析模型(InterventionAnalysisMode1)是由美国威斯康辛大学的博克斯教授和刁锦寰教授(BoxAndTiao)于2O世纪7O年代提出的一种时间序列分析模型。这种方法始于对美国西海岸洛杉矶大气污染的环境问题的研究,此后引起众多经济学家的重视,被广泛应用于经济政策的变化或突发事件(战争爆发、罢工、广告促销等)给经济带来影响的定量分析。在国内,有学者将这种分析方法应用于研究我国农村经济体制改革的实效、物价波动的干预效用问题,但如何将这种分析方法运用于分析宏观经济政策冲击对我国钢铁产品市场对我国股票市场的影响则还没有。
干预模型是时间序列分析中传递函数模型的一种推广。在干预模型模型,干预变量是模型的基本变量。所谓干预变量,是代表干预的一种虚拟变量,它作为模型的输入变量来解释干预事件对响应变量的影响。常用的干预变量有两种:一种是一但发生就会产生长期影响的持续干预变量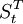 ;另一种是发生后只有短暂性影响的暂时性干预变量
;另一种是发生后只有短暂性影响的暂时性干预变量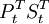 可用一个阶梯函数来表示:。
可用一个阶梯函数来表示:。
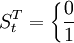
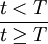
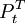 可以表示为一个脉冲函数:
可以表示为一个脉冲函数:
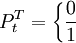
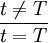
式中T表示干干预事件发生的时间。上述两类干预变量虽然表示形式不同,但它们之间有如下的内在联系: 。
。
B为后移算子。
在现实中,干预事件的影响形式可以有多种形式,但按其影响的特点,可以归纳出如下四种基本类型:
(1)影响突然开始且长期持续下去: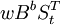
(2)影响缓慢开始,然后长期持续下:
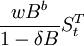 。当δ = 0时,干预的影响只存在一个时期;当δ = 1时,干预的影响将长期存在;当0 < δ < 1时,干预的影响以速度渐进衰减,最后回到干预前的水平。
。当δ = 0时,干预的影响只存在一个时期;当δ = 1时,干预的影响将长期存在;当0 < δ < 1时,干预的影响以速度渐进衰减,最后回到干预前的水平。
(4)影响缓慢开始,持续时间短暂:

在较复杂的情况时,可以将上面的四种模型都组合起来
一般地,干预模型具有下面的形式:
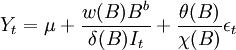 。
。
其中,B为后移算子,εt为白噪声序列,B^b表示干预影响延迟b期才起作用,当b=0,表示干预事件一出现就立即产生影响。It代表干预变量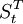 或。
或。
模型的待估参数为:
w = (w0,w1,Μ,ws),δ = (δ1,δ2,Μδr),θ = θ1,θ2,Μθq),χ = χ1,χ2,Μχp)。
从中国钢铁产品市场价格的实际数据来看,每次宏观经济政策的出台,都会对市场价格产生突然冲击,然后长期持续下去。因此,这里选择如下形式的干预模型:
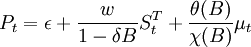 。
。
二、干预分析模型的识别与参数估计
利用干预影响产生前(1998年3月至2005年4月)的数据,即宏观调控政策出台前的市场价格数据,建立一个单变量的ARIMA模型(自回归求积移动平均Austoreg Ressive Integrated MovingAverage缩写为ARIMA)。然后,利用此模型进行趋势外推预测,得到的预测值,作为不受干预影响的数值。最后将实际值减去这些预测值,得到的是受干预影响的的具体结果。利用这些结果可以估计干预模型的参数。
(一)建立一个单变量的ARIMA模型
1.数据的处理
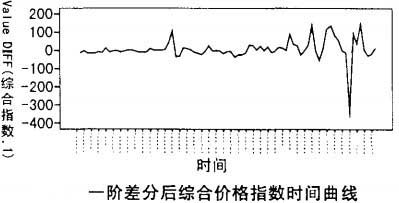
观察图1所视综合价格指数时间曲线,发现数据非平稳含有明显的趋势项。对数据进行一阶差分,数据即变为平稳随机序列,如下图:
2.ARIMA(P,d,q)模型的识别
所谓模型的识别,即根据所要处理的数据序列的统计特征,来确定P、d和q的值。
由前面所述,一阶差分后价格综合指数的趋势就消除了,因此d=1。
在实际识别ARIMA(p,q)模型时,需多次反复偿试,有可能存在不止一组(p,q)值都能通过识别检验。
显然,增加P与q的阶数,可增加拟合优度,但却同时降低了自由度。
因此,对可能的适当的模型,存在着模型的“简洁性”与模型的拟合优度的权衡选择问题。通常,ARMA(p,q)过程的偏自相关函数(PACF)可能在P阶滞后前有几项明显的尖柱(spikes),但从P阶滞后项开始逐渐趋向于零。而它的自相关函数(ACF)则是在q阶滞后前有几项明显的尖柱,从q阶滞后项开始逐渐趋向于零。
因此,用一阶差分后的数据偏相关系数判别P,用自噪音。
相关系数判别q,得出(P,q)的所有可能取值。其中,P由显著不为零的偏相关系数的数据决定;q由显著不为零的自相关系数的数据决定。
将综合价格指数一阶差分后的数据输入SPSS计算ACF-PACF得到优化后的结果:p=3,q=0。
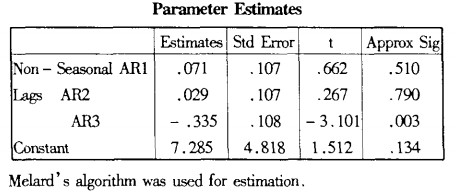
3.ARIMA(P,d,q)的参数识别。
将上面求得的P、d、q和综合价格指数数据输入SPSS计算模型参数如下:
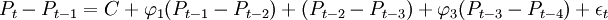 。
。
移项得:P_t=C(1+\varphi_1)P_{t-1}+(\varphi_2-\varphi_1)P_{t-2}+(\varphi_3-\varphi_2)P_{t-3}-\varphi_3P_{t-4})+\epsilon_t。
将\varphi_1=AR1、\varphi_1=AR2、\varphi_1=AR3代入上式得:P_{t1}=7.285+1.071P_{t-1}-0.042P_{t-2}-0.364P_{t-3}+0.335P_{t-4}+\epsilon_t。
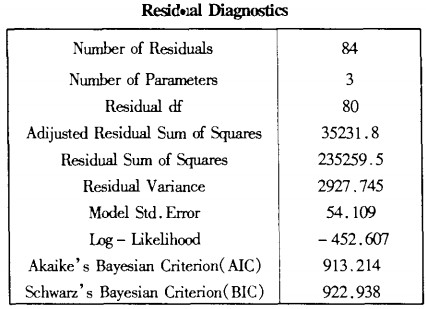
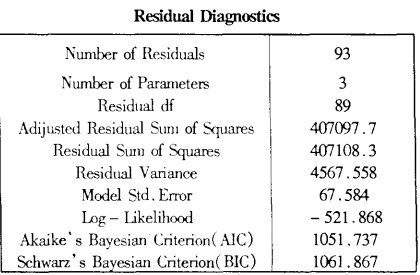
4.ARIMA(P,d,q)的模型检验由于ARIMA(P,d,q)模型的识别与估计是在假设随机扰动项是白噪声的基础上进行的,因此,如果估计的模型确认正确的话,残差εt应代表一白噪声序列。
如果通过所估计的模型计算的样本残差不代表一白噪声,则说明模型的识别与估计有误,需重新识别与估计。
在实际检验时,主要检验残差序列是否存在自相关
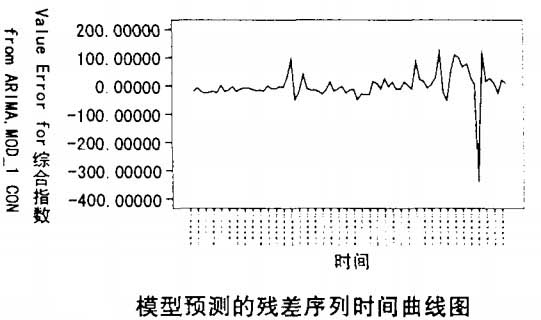
将上述A脚MA(3,1,0)得到的预测值与实际值的残差序列求算术平均值为-0.1761752,基本接近零均值。
残差序列时间线图如下,没有趋势项,类似随机白噪音
(二)建立干预分析模型
1.干预模型参数的估计
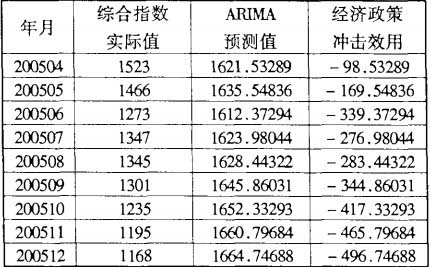
运用ARIMA(3,1,0)模型对2005年4月到12月的市场价格数据进行外推预测,然后用实际值减去预测值,得到的差值就是宏观调控政策所产生的冲击效用,记为Zt。
利用上表数据可以估计处干预模型的参数:
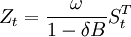
其中,当t<86时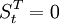 ,当t≥86时
,当t≥86时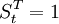 。参数估计如下:
。参数估计如下:
ω = − 307.057,δ = 0.873。
2.计算净化序列并建立新的ARIMA模型
净化序列是指消除了干预影响的序列,它由实际的观察值序列减去干预影响值得到:
 。
。
Pt为消去了干预影响的净化序列。同样对净化序列求ARNA(3,1,0)模型如下:
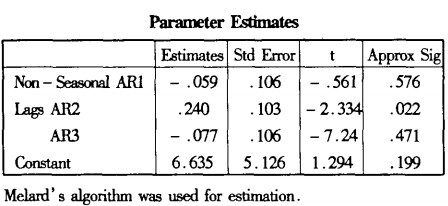
Pt2 = 6.635 + 0.041Pt − 1 − 0.181Pt − 2 + 0.163Pt − 3 + 0.077Pt − 4 + εt
3.组建干预分析模型
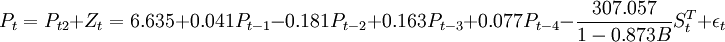 。
。
其中,当t<86(2005年4月)时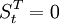 ,当t≥86时(2005年4月)
,当t≥86时(2005年4月)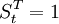
(4)干预分析模型的检验
平均绝对差: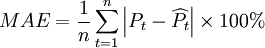 。
。
平均绝对差率: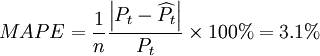 。
。
均方根误差:![RMSE=\sqrt{\frac{1}{n}\sum_{t=1}^n[P_t-\widehat{P_t}]^2}=65.76](/w/images/math/8/6/3/863e85d83b9eceb33192b9d6115bd7d4.png) 。
。
模型拟合度: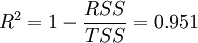
钢铁产品市场是生产资料市场,其价格的变化除了受供求关系等市场规律的影响,还直接受到国家宏观经济政策的外在冲击(最终也表现为供求的影响)。干预模型是定量分析宏观经济政策影响对钢铁产品市场冲击效用的有效手段之一。
- ↑ 谢向前.中国钢铁产品市场价格干预分析模型研究[J].武汉冶金管理学院学报.2006(3)
评论(共8条)
你好,不好意思那么冒昧的打扰你,我是一名学生,看到你的博客里关于干涉预测模型的解算方法,我这一个多月都在研究这个算法,但是遇到了很大的困难,想咨询一下你关于这个算法里面的参数要怎么解算?想问下怎么方面能和你直接联系你,十分感谢了
你学过计量吗?学过的话,这些数据都是利用回归,最小二乘法在Eviews里运行得出
你好,我做毕业论文也需要用到干预分析模型,不明白ω = − 307.057,δ = 0.873是怎么估计出来的,真心向您请教
模型Z_t=ω/(1-δB) S_t^T中,S_t^T=1,因此相当于估计Z_t=ω/(1-δB)即(1-δB)*Z_t=ω,即Z_t-δB*Z_t=ω,即Z_t=δB*Z_t+ω,即Z_t=δZ_(t-1)+ω,相当于做一个AR(1)模型,用最大似然估计,就可得到上述得数
你好我使用AR(1)拟合的干预模型是斜向下的直线,但是我的干预值呈现V字形,感觉很不对,是哪里出现问题了吗
你好,我做毕业论文也需要用到干预分析模型,不明白ω = − 307.057,δ = 0.873是怎么估计出来的,真心向您请教
加一










你好,不好意思那么冒昧的打扰你,我是一名学生,看到你的博客里关于干涉预测模型的解算方法,我这一个多月都在研究这个算法,但是遇到了很大的困难,想咨询一下你关于这个算法里面的参数要怎么解算?想问下怎么方面能和你直接联系你,十分感谢了