单因子模型

出自 MBA智库百科(https://wiki.mbalib.com/)

单因子模型(One factor model)

　　单因子模型最早由威廉·夏普(Sharp)提出；

　　单因子模型的基本思路是：证券收益只受一个因素影响。市场模型便是这种模型的典型例子。如果我们观察证券市场，就会发现，当市场股价指数上涨时，大部分股票价格也同时上涨；反之亦然。这说明，各种证券对一个因子，即市场股价指数的变化具有联动的反应。

　　R_i = α_i + β_iF + ε_i　　(1)

　　其中，F是共同因子的预测值，β_i为证券i对因子的灵敏度。如果因子预测值为零，证券收益等于α_i + ε_i。ε_i是一个随机误差项，其预期值为零，标准差为σ_εi。

　　单因子模型有两个重要的假设：

　　(1)随机误差项和因子项互不相关，也就是因子对随机误差项的结果没有任何影响，它们之间的协方差Cov(ε_i,F) = 0。

　　(2)任何两种证券的随机误差项互不相关，也就是一种证券的随机误差项的结果对其它任何一种证券的随机误差项的结果没有任何影响，它们之间的协方差COv(ε_i,ε_j) = 0。这意味着各种证券有规则地同步运动仅仅是因为它们对共同因子所作出的反应。

　　如果上述两个假设中的任何一个不成立的话，那么这种单因子模型只是一个近似模型；从理论上讲，其它类型的模型(也可能是一种多因子模型)也许能够更准确地描述证券收益创造过程。

　　根据单因子模型，证券i的预期收益可表示为

　　E(R_i) = α_i + β_iE(F)　　(2)

　　而证券i的收益率的方差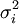等于：

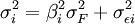　　 　　(3)

　　其中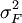，是共同因子F的方差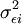，是随机误差项ε_i的方差。由等式(3)可知，任何一种证券的风险可分为两个部分：无法分散掉的因子风险于和通过分散化投资可以被消除的非因子风险。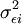

　　又根据单因子模型，任何两种证券之间的协方差可表示为：

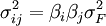　　　　(4)

　　如果一种证券的单因子模型成立，那么由几种证券组成的证券组合的预期收益可表示为：

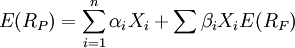　　　　(5)

　　其中，E(R_P)表示证券组合的预期收益，X_i为证券组合中i种证券的权重。而证券组合的方差σ_P等于：

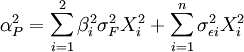　　　　(6)

　　由等式(5)和(6)可知，只要估算出每种证券的α_i、β_i和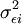值，以及共同因子预期收益E(F)及其方差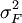，我们就能计算出证券组合的预期收益和方差。因此，估算由几种证券组成的证券组合所需要的估测值数目为3n+2，较利用马柯维茨方法选择最佳证券组合大大地简化了。

　　(1)切点证券组合

　　单因子模型假定所有的证券收益仅仅对单个共同因子的变化作出反应，省去了直接估算证券间协方差的作业(因为这些协方差包含在证券对共同因子灵敏度和共同因子方差之中)，因而大大简化了确定切点证券组合的手续。

　　利用单因子模型，投资者可以估算几种证券中的每一种证券的α_i、β_i和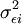，以及因子F的预期值E(F)及其方差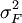。有了这些估算值，并根据等式(2)、(3)和(4)，便可计算出证券的预期收益、方差和协方差。接下来，投资者可以利用最优化法，计算出马柯维茨有效集；根据已知的无风险利率，确定切点证券组合。

　　(2)多样化

　　市场模型告诉我们，通过分散投资可以使市场风险平均化，并降低证券组合的独有风险。对于任何单因子模型，只要用因子风险和非因子风险分别替代市场模型中的市场风险和独有风险，便可得出同样的结论。等式(3)中的和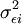分别称为证券i的因子风险和非因子风险。

　　当一个证券组合越分散，也就是包含的证券种类越多，分配到每一种证券在证券组合中所占的比例X_i，也就越小。除非投资者刻意搭配证券组合中不同β值的证券，分散投资并不能使证券组合的β值显著地增加或减少，如等式(6)所示，证券组合的β值只是各证券β值的加权平均，权重为各证券所占的投资比重，因而分散投资只能使因子风险平均化。

　　可是，当证券组合越分散，有理由期待非因子风险也随之降低。假设n种证券组成的证券组合中每一种证券的权重X_i都相同．即X_i等于1/n，则等式(6)可改写为：

　　(7)

　　其中方括弧内的值是各证券非因子风险的加权平均。但证券组合的非因子风险只是它的n分之一。当证券组合越分散，证券的种数n也就越大；相反地，1/n值则越小，因而降低证券组合的非因子风险。总之，通过分散投资可以降低非因子风险。

　　单因子模型形式简便，参数的个数少，容易估计，并且应用起来也比较简单

• 单因子模型的灵活性较差， 难以反映实际的各种可能的零息债券的收益曲线和利率期限结构的动态。

• 单因子模型隐含地假定所有可能的零息债券利率之间是完全相关的。

• 利用单因子模型对短期债券定价的误差是比较小的。

• 多因子模型