主成分分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
主成分分析(principal components analysis,PCA)又称:主分量分析,主成分回归分析法
目录 |
主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在统计学中,主成分分析(principal components analysis,PCA)是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分往往能够保留住数据的最重要方面。但是,这也不是一定的,要视具体应用而定。
在实证问题研究中,为了全面、系统地分析问题,我们必须考虑众多影响因素。这些涉及的因素一般称为指标,在多元统计分析中也称为变量。因为每个变量都在不同程度上反映了所研究问题的某些信息,并且指标之间彼此有一定的相关性,因而所得的统计数据反映的信息在一定程度上有重叠。在用统计方法研究多变量问题时,变量太多会增加计算量和增加分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。主成分分析正是适应这一要求产生的,是解决这类题的理想工具。
同样,在科普效果评估的过程中也存在着这样的问题。科普效果是很难具体量化的。在实际评估工作中,我们常常会选用几个有代表性的综合指标,采用打分的方法来进行评估,故综合指标的选取是个重点和难点。如上所述,主成分分析法正是解决这一问题的理想工具。因为评估所涉及的众多变量之间既然有一定的相关性,就必然存在着起支配作用的因素。根据这一点,通过对原始变量相关矩阵内部结构 的关系研究,找出影响科普效果某一要素的几个综合指标,使综合指标为原来变量的线性拟合。这样,综合指标不仅保留了原始变量的主要信息,且彼此间不相关,又比原始变量具有某些更优越的性质,就使我们在研究复杂的科普效果评估问题时,容易抓住主要矛盾。 上述想法可进一步概述为:设某科普效果评估要素涉及个指标,这指标构成的维随机向量为。对作正交变换,令其中为正交阵的各分量是不相关的,使得的各分量在某个评估要素中的作用容易解释,这就使得我们有可能从主分量中选择主要成分,削除对这一要素影响微弱的部分,通过对主分量的重点分析,达到对原始变量进行分析的目的。各分量是原始变量线性组合,不同的分量表示原始变量之间不同的影响关系。由于这些基本关系很可能与特定的作用过程相联系,主成分分析使我们能从错综复杂的科普评估要素的众多指标中,找出一些主要成分,以便有效地利用大量统计数据,进行科普效果评估分析,使我们在研究科普效果评估问题中,可能得到深层次的一些启发,把科普效果评估研究引向深入。
例如,在对科普产品开发和利用这一要素的评估中,涉及科普创作人数百万人、科 普作品发行量百万人、科普产业化(科普示范基地数百万人)等多项指标。经过主成分分析计算,最后确定个或个主成分作为综合评价科普产品利用和开发的综合指标,变量数减少,并达到一定的可信度,就容易进行科普效果的评估。
主成分分析法是一种降维的统计方法,它借助于一个正交变换,将其分量相关的原随机向量转化成其分量不相关的新随机向量,这在代数上表现为将原随机向量的协方差阵变换成对角形阵,在几何上表现为将原坐标系变换成新的正交坐标系,使之指向样本点散布最开的p 个正交方向,然后对多维变量系统进行降维处理,使之能以一个较高的精度转换成低维变量系统,再通过构造适当的价值函数,进一步把低维系统转化成一维系统。
主成分分析的原理是设法将原来变量重新组合成一组新的相互无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上处理降维的一种方法。主成分分析是设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。通常数学上的处理就是将原来P个指标作线性组合,作为新的综合指标。最经典的做法就是用F1(选取的第一个线性组合,即第一个综合指标)的方差来表达,即Va(rF1)越大,表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2即选第二个线性组合,为了有效地反映原来信息,F1已有的信息就不需要再出现再F2中,用数学语言表达就是要求Cov(F1,F2)=0,则称F2为第二主成分,依此类推可以构造出第三、第四,……,第P个主成分。[1]
概括起来说,主成分分析主要由以下几个方面的作用。
1.主成分分析能降低所研究的数据空间的维数。即用研究m维的Y空间代替p维的X空间(m<p),而低维的Y空间代替 高维的x空间所损失的信息很少。即:使只有一个主成分Yl(即 m=1)时,这个Yl仍是使用全部X变量(p个)得到的。例如要计算Yl的均值也得使用全部x的均值。在所选的前m个主成分中,如果某个Xi的系数全部近似于零的话,就可以把这个Xi删除,这也是一种删除多余变量的方法。
2.有时可通过因子负荷aij的结论,弄清X变量间的某些关系。
3.多维数据的一种图形表示方法。我们知道当维数大于3时便不能画出几何图形,多元统计研究的问题大都多于3个变量。要把研究的问题用图形表示出来是不可能的。然而,经过主成分分析后,我们可以选取前两个主成分或其中某两个主成分,根据主成分的得分,画出n个样品在二维平面上的分布况,由图形可直观地看出各样品在主分量中的地位,进而还可以对样本进行分类处理,可以由图形发现远离大多数样本点的离群点。
4.由主成分分析法构造回归模型。即把各主成分作为新自变量代替原来自变量x做回归分析。
5.用主成分分析筛选回归变量。回归变量的选择有着重的实际意义,为了使模型本身易于做结构分析、控制和预报,好从原始变量所构成的子集合中选择最佳变量,构成最佳变量集合。用主成分分析筛选变量,可以用较少的计算量来选择量,获得选择最佳变量子集合的效果。
1、原始指标数据的标准化采集p 维随机向量x = (x1,X2,...,Xp)T)n 个样品xi = (xi1,xi2,...,xip)T ,i=1,2,…,n,
n>p,构造样本阵,对样本阵元进行如下标准化变换:
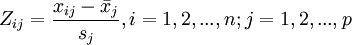
其中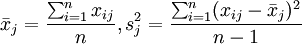 ,得标准化阵Z。
,得标准化阵Z。
2、对标准化阵Z 求相关系数矩阵
![R=\left[r_{ij}\right]_pxp=\frac{Z^T Z}{n-1}](/w/images/math/7/e/4/7e473cd0da3efb71ab376cb9ed048e72.png)
其中, 。
。
3、解样本相关矩阵R 的特征方程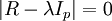 得p 个特征根,确定主成分
得p 个特征根,确定主成分
按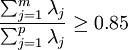 确定m 值,使信息的利用率达85%以上,对每个λj, j=1,2,...,m, 解方程组Rb = λjb得单位特征向量
确定m 值,使信息的利用率达85%以上,对每个λj, j=1,2,...,m, 解方程组Rb = λjb得单位特征向量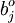 。
。
4、将标准化后的指标变量转换为主成分
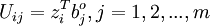
U1称为第一主成分,U2 称为第二主成分,…,Up 称为第p 主成分。
5 、对m 个主成分进行综合评价
对m 个主成分进行加权求和,即得最终评价值,权数为每个主成分的方差贡献率。
优点:
①可消除评估指标之间的相关影响。因为主成分分析法在对原始数据指标变量进行变换后形成了彼此相互独立的主成分,而且实践证明指标间相关程度越高,主成分分析效果越好。
②可减少指标选择的工作量,对于其他评估方法,由于难以消除评估指标间的相关影响,所以选择指标时要花费不少精力,而主成分分析法由于可以消除这种相关影响,所以在指标选择上相对容易些。
③主成分分析中各主成分是按方差大小依次排列顺序的,在分析问题时,可以舍弃一部分主成分,只取前面方差较大的几个主成分来代表原变量,从而减少了计算工作量。用主成分分析法作综合评估时,由于选择的原则是累计贡献率≥85%,不至于因为节省了工作量却把关键指标漏掉而影响评估结果。
缺点:
①在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平(即变量降维后的信息量须保持在一个较高水平上),其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释(否则主成分将空有信息量而无实际含义)。
②主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价。因此,提取的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。
③当主成分的因子负荷的符号有正有负时,综合评价函数意义就不明确。
案例一:主成分分析法在啤酒风味评价分析中的应用[2]
啤酒是个多指标风味食品, 为了全面了解啤酒的风味, 啤酒企业开发了大量的检测方法用于分析啤酒的指标, 但是面对大量的指标数据, 大多数企业又感到茫然,不知道如何利用这些大量的数据, 由上面的介绍可知,在这种情况下,主成分分析法能够派上用场。近年来,科研人员为了获得对啤酒风味更好的理解, 多元统计技术的使用越来越多。这主要有以下两方面的原因:①在啤酒领域里, 几乎没有一个问题能够使用单变量(单指标)就能反映事物的属性, 例如啤酒的好坏、一致性, 不能通过双乙酰一个指标说明问题;②另一个重要的原因就是, 近年来大量数学统计软件的不断出现和个人电脑的普及促进了多元统计分析技术的应用。多元统计技术在啤酒风味研究中的一个重要任务就是找出啤酒风格和啤酒理化指标(风味成分指标也属于理化指标)之间的相关性。例如可以用多元统计技术来找出啤酒的风味指标和啤酒风味的关系或不同啤酒的风味差异性。
经常使用的多元统计技术有聚类分析、判别分析、主成分分析和回归分析等。其中主成分分析能够用于多指标产品, 主成分分析可以按照事物的相似性区分产品, 结果可用一维、二维或三维平面坐标图标示, 特别直观。使用主成分分析法可以研究隐藏在不同变量背后的关系,而且根据这些变量能够获得主成分的背景解释。
鉴于主成分分析在啤酒风味质量应用中的强大作用, 本文简单介绍主成分分析的基本原理及其在啤酒一致性监控中的应用,以引起我国啤酒同行的广泛关注。
1.1 仪器
HP 6890 毛细管气相色谱仪 (美国安捷伦公司),FID 检测器, HP 7694E 顶空自动进样器, HP 气相色谱化学工作站。
1.2 分析方法
1.2.1 样品制备
啤酒于5 ℃冷藏, 量取 5 mL 酒液于 20 mL 顶空瓶中, 添加2.0 g/L 正丁醇溶液 0.10 mL, 加密封垫及铝盖密封,振荡混匀以供顶空气相色谱测定。
1.2.2 色谱条件
毛细管色谱柱 (DB- WAXETR 30 m×0.53 mm i.d,膜厚1.0 μm);柱温:起始温度为 35 ℃, 以 10 ℃/min 程序升温至150 ℃, 再以 20 ℃/min 升温到180 ℃, 并继续恒温5 min;进样口温度 150 ℃; 检测器温度 200 ℃; 载气为高纯氮气, 流速为5 mL/min;氢气 30 mL/min;空气400 mL/min;采用分流进样,分流比为1∶1。
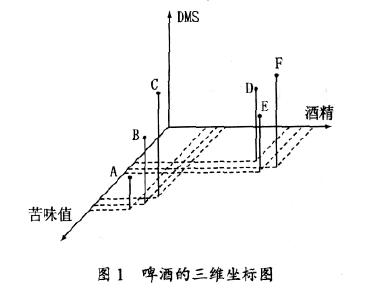
2.1 主成分分析法在啤酒研究中应用的必要性这里通过一个例子说明, 主成分分析在啤酒研究中的必要性。假如有6 个啤酒样品,分别标为A- F,每个啤酒样品用3 个指标来描述。这些指标可以是仪器的分析数据、感官分析数据或两者都用。为了便于讨论,假设这3 个指标分别为苦味值(BU)、DMS和酒精浓度。为了解这6 个样品两两之间的相似性, 便于将这6 个样品进行分类,可以把这6 个样品画在三维空间中,见图1。显然在这个简单的例子中, 这6 个样品倾向于形成两类, 即分别是A- C 和 D- F。通过所测的指标可以解释这种分类, 例如, 第一组(A- C)有较高的苦味值和较低的酒精浓度。这个例子中只涉及到6 个样品和3 个指标。但是实际上, 样品数量和指标数量都会很大, 例如, 有20 个指标, 这时, 样品不能在20 维的坐标系中画出。为了解决多指标的样品的比较问题,可以使用主成分分析法。
2.2 主成分分析法的基本原理
主成分分析的第一步是将所有的指标数据进行标准化, 标准化的一般方法为: (xij − xjmean) / δj, 这里xij是样品i 的第 j 个指标, xjmean 和 δj是第j 个指标的平均值和标准偏差, 通过标准化后, 每个变量的平均值变成0,标准偏差为1。标准化的好处是可以消除不同指标间的量纲差异和数量级间的差异。
第二步求出指标间的相关矩阵, 通过相关矩阵, 可以确定具有高度相关性的指标, 这些指标间的协方差可以通过另一个变量替代, 这个变量叫作第一成分。去掉第一成分后, 计算残留相关阵, 通过残留相关阵, 第二组高度相关的变量也可以发现, 它们的协方差可以用第二成分替代, 第二成分和第一成分是正交的。第二成分对原始数据的贡献去除后, 可以提取第三成分。此过程一直继续, 直到原始数据的所有方差都被提取后结束。结果是原数据转化成了同样数量的新变量, 但是, 这些新变量之间是正交的。
因此, 每个样品的原始变量的标准化数据就被转换成一系列成分的计算值。每一个样品, 原始数据能够表达成新成分的线性组合值, 例如一个有9 个指标的数据集就可转换成:
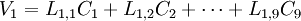
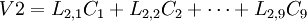
………………
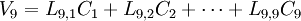
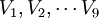 是原始数据的标准化值。
是原始数据的标准化值。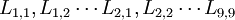 是原变量与新成分之间的相关程度的指标, 一般将其称为因子荷载。
是原变量与新成分之间的相关程度的指标, 一般将其称为因子荷载。
通过计算机的主成分程序生成对方差的贡献率。一般而言, 原数据的总方差总是高度集中在前几个成分中。因此,在这个分析中,可以基于可以接受的最低方差贡献率,来选择几个数目较少的主成分。最终,可以用选择的几个主成分来重新计算所用的样品。重新计算的值叫做主成分得分。
因为原始数据阵的方差通常集中在前几个主成分中(一般为2 或 3 个), 因此样品的一系列标准化因子得分可以在二维的平面坐标中画出, 这样就能够根据样品的相似性来分类样品。另外, 还可以根据因子荷载对这种分类做出某种解释。
3.1 主成分分析法在不同品牌啤酒风味差异性评价中的应用
啤酒是含酒精的饮料酒, 啤酒的风味是人们选择啤酒的主要影响因素。显然啤酒不同于同浓度的酒精水溶液, 主要是因为啤酒除了含有酒精外还含有数以百计的微量成分, 例如醛、醇及酯类等。对于啤酒生产企业来说, 把自己的啤酒和竞争啤酒的风味进行比较非常重要, 这样可以了解自己的啤酒和竞品的差异, 分析竞争啤酒受市场欢迎的原因, 以改进自己的产品, 或者找出自己啤酒的风格特点, 走差异化竞争之路。为了完成此工作, 啤酒企业可以把自己的啤酒和竞争啤酒进行对比品评, 这是一种非常好的方法, 但是此方法很难从本质上找到与竞品的差异, 很难形成指导生产的定性定量措施。为了解决此问题, 啤酒企业可以对啤酒的风味成分进行分析, 理论上讲, 分析的成分越多, 获得的信息量越大, 但是, 很难从总体上进行对比分析, 这时, 可以通过主成分分析法, 提取主要的综合成分, 然后在平面坐标系中画图进行比较。
图2 是我国市场上主要啤酒的风味物质经主成分分析后的前两个主成分的平面坐标。分析的风味成分有乙醛、乙酸乙酯、异丁酯、乙酸异戊酯、异戊醇及己酸乙酯。分析的时间跨度为半年, 这些数据通过主成分分析法后, 提取前两个主成分, 这两个主成分可以反映全部信息的83.1 %, 提取较为完全, 这说明这两个主成分替代原始的6 个风味成分反映的样品信息。百威啤酒、喜力啤酒和青岛啤酒是我国啤酒市场上的3 种知名品牌,同时这3 种啤酒的质量也是得到人们的认可的。
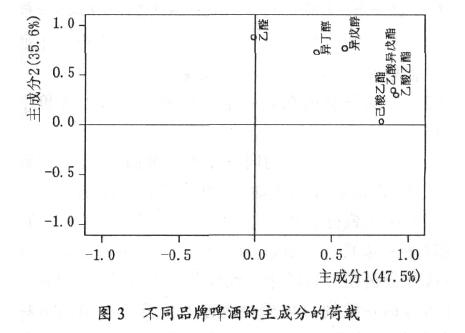
从图2 可看出, 尽管百威啤酒、喜力啤酒和青岛啤酒随着时间的变化每种啤酒的风味成分的含量有所波动, 但是, 每种啤酒还是各自成一团, 自成一类, 三者的中心犹如一个三角形的3 个顶点, 三者组成一个风味三角形。从图2 还可看出, 南方某品牌的啤酒有独自成型的特点, 即其不同于青岛啤酒、也不同喜力啤酒和百威啤酒的风格,实际上通过感官品尝也可以得到此结论。主成分分析法采用的分类是可以通过对主成分的分析做出解释的,图3 是前两个主成分的因子荷载图。
从图3 可以看出, 主成分 1 主要由乙酸乙酯、乙酸异戊酯和己酸乙酯决定, 这些酯含量高, 主成分1 就越大, 即主成分1 代表了啤酒的酯香, 酯香越浓, 主成分 1就越大。主成分2 主要由乙醛、异丁醇和异戊醇决定,这些成分能够代表啤酒的“酒劲”的大小, 这些成分含量越高,主成分2 就越大,即啤酒的酒味就越重。结合这种解释, 就可以对图2 中的分类做出分析, 其中百威啤酒是酒味适中和酯香相对较浓的“浓香型”啤酒, 喜力啤酒是酒味和酯香均较浓的“浓醇型”啤酒, 青岛啤酒是酒味较重, 而酯香较弱的“醇型”啤酒, 而某品牌的啤酒则是酒味和酯香均弱的“淡型”啤酒。
3.2 主成分分析法在同一品牌啤酒风味一致性评价中的应用
3.2.1 主成分分析法在同一品牌不同生产厂之间一致性评价中的应用
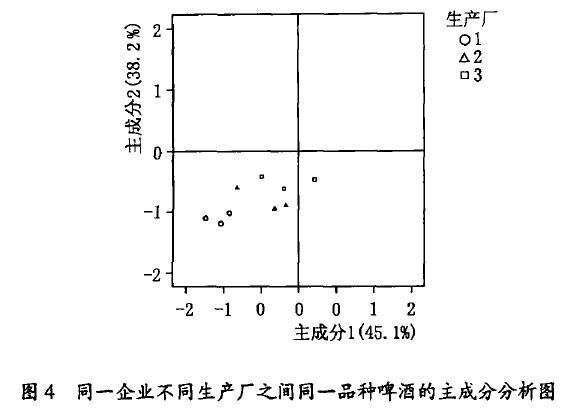
近十几年来, 我国啤酒行业发展非常快, 啤酒企业的规模越来越大, 很多啤酒企业已经走出啤酒的“原产地”到异地建厂,进一步扩大企业的规模。对于一些啤酒企业来说, 新建厂面对的消费群体和建厂前面对的消费群体较为一致, 这时就要求新建厂生产的啤酒要与原厂生产的啤酒风格一致, 以免生产厂在切换时, 消费者不认可的情况发生。图4 是同一企业的3 个不同生产厂之间的同一品种啤酒的主成分分析图。
从图4 可以看出, 总的来说, 3 个生产厂生产的啤酒还是比较一致的, 因为3 个厂生产的同一品种的啤酒的波动范围较小。从图4 还可以看出, 生产厂1 因为生产的历史长, 生产较稳定, 因此其波动较小(图中的圆圈);生产厂2 和生产厂3 的稳定性就稍差一点, 这是由于这两个厂都是新厂,有个磨合的过程。同时,生产厂2
和生产厂1 的风味较为一致, 生产厂 3 和生产厂1 的一致性就稍差,其中生产厂3 是最新的厂。
3.2.2 主成分分析在同一生产厂啤酒一致性评价中的应用
同一生产厂生产的同一品种的啤酒, 由于不同时间的水质、原辅料等的波动, 最终体现在产品风味的波动上。同一主成分分析也可以评价产品随时间的一致性。现以某一啤酒企业2006 年生产的某品种啤酒为例说明主成分分析在产品风味一致性评价中的应用。要评价啤酒风味的一致性, 啤酒企业首先要测定啤酒的风味指标,目前通过顶空-毛细管技术能测定大约10 种的风味物质,分别为乙醛、DMS、甲酸乙酯、乙酸乙酯、乙酸异丁酯、正丙醇、异丁醇、乙酸异戊酯、异戊醇和己酸乙酯。以前的一些统计技术例如统计过程控制(SPC)的控制图等只能说明某一指标的波动情况, 而不能从总体上反映产品的波动性, 因为有些指标的波动, 不会引起产品风格的波动, 而主成分分析法, 是从总体上说明产品的波动性,比控制图更能说明产品的波动性。
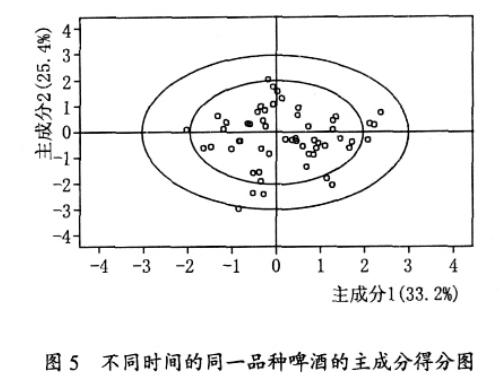
图5 是某啤酒企业 2006 年一年生产的某品种的啤酒的10 种风味指标的前两个主成分的平面坐标图,这两个主成分可反映产品约60 %的信息。图 5 中的第一个小椭圆是95 %的置信区, 即在这个椭圆外的点占5 %, 通过对该椭圆外的点进行跟进分析可以发现波动的原因, 并在以后的生产过程中加以避免, 以提高产品的一致性。
4.1 主成分分析法, 可以消除各变量之间的共线性, 减少变量的个数,利于后续的分析。
4.2 使用主成分分析可以按照事物的相似性区分产品, 结果可用一维、二维或三维平面坐标图标示, 特别直观。
4.3 将样品的数据通过主成分分析进行浓缩, 然后通过平面坐标可以实现从总体上对样品进行一致性的分析,一般的统计技术只能对某一指标进行评价。
4.4 静态顶空进样高效毛细管气相色谱分析啤酒香味组分技术结合, 主成分分析技术可以有效地应用于评价不同品牌啤酒风味的差异性、同一啤酒的风味一致性与均一性。
案例二:主成分分析法在食品领域的应用[1]
一、在食品风味方面的应用
目前,主成分分析应用还是比较广泛的,但是就食品风味方面,关于该分析方法的文献鲜见报道。戴素贤等人对七种高香型乌龙茶中的香气成分进行了主成分分析,他们尝试用主成分分析法来研究茶业香型的变化,并进而找到影响这些香型变化的主要化合物,同时还发现了不同的茶别中香气化合物变化的趋势并进行了模拟量化,直观地表现了各种香气化合物对香气的贡献程度。李华等运用多元统计分析确定葡萄酒感官特性,多元统计分析中的主成分分析等数学工具能够把大量的描述葡萄酒感官特性的描述语精简成较少的综合性更强的描述语,这些精简后的描述语不但能够反映精简前描述语的信息,还可以筛选出科学合理的描述符,描述符是描述分析的语言和应用主成分分析法完成了不同品牌啤酒风味差异性的评价,同一品牌啤酒风味一致性的评价,同一品牌不同生产厂之间一致性的评价以及同一生产厂啤酒一致性的评价这些工作。啤酒是个多指标的风味食品,主成分分析法可以帮助我们更好地研究啤酒理化指标和啤酒风格之间的相关性,从而达到更好地理解啤酒风味的目的。岳田利等人则通过利用主成分分析的方法建立了苹果酒香气质量的评价模型,并以此来对苹果酒样品香气组分进行客观的统计分析。S.Kallithraka等采用高效液相色谱法和气相色谱法研究了希腊国内不同产地葡萄酒的化合物成分和感官特性,并运用了PCA法(主成分分析法)对所得参数进行多元分析,最终达到给葡萄酒评价和分类的目的。
二、在食品品质方面的应用
食品品质的评价往往是非常复杂的过程。因为影响食品品质的因素大量存在,非人为因素如食品环境中的微生物,温度及pH等的变化带来的影响。另一方面,由于人为的因素掺假也会造成食品品质的低劣,进而损害广大销售者和消费者的利益。如黎海红等人运用主成分分析法对掺伪芝麻油的检测方法进行研究分析。根据主成分分析的实验原理,可以选择芝麻油的折光率、酸价、色泽、水分及挥发物、皂化值和碘价等理化指标作为变量,将这些变量的所测数据做矩阵处理最后分析就能知道掺伪芝麻油的主成分及其贡献率。我们知道,芝麻油掺杂了其他的植物油,其理化指标就会出现变化,这是质量鉴别的基础和依据。利用主成分分析可以从大量的数据中提取与芝麻油掺伪相关的有用的信息,最终可以较好地区分掺杂有其他植物油的芝麻油。采用主成分分析方法还可以评价分析面条的品质,面条品质的感官评价存在着一定的缺陷,在面条品质评价的过程中,需要对大量的待测样本属性进行测量,在这些属性中有一些是由相互关联的数据组成的,如面条的韧性会影响面条的拉断力和平均拉力,因此,拉断力和平均拉力是相关的,倘若在预测韧性的相应等式中同时用到了拉断力和平均拉力,那么预测出的韧性要比实际韧性大,因为进行了重复计算,所以一定要确保等式中的变量之间尽可能地保持独立,主成分分析在这样的情况下通过对一组影响某一问题的相关变量进行线性变换,使得变换后得到的变量独立不相关就叫做主成分,这样的主成分不仅保留了原来相关变量中的主要信息,彼此间又不相关。面条品质通过主成分分析法得到的综合评价与主观评价(外观、色泽、适口性、咬劲、弹性、黏性、食味等)有相似之处,但是它比主观评价更加细化,对具体样本进行了量化,为面条品质的进一步分析提供了可靠的参考依据。
主成分分析法还可以应用于保健食品功能学评价的研究,评价保健食品的功能特性—对抗疲劳和耐缺氧作用。利用主成分分析对包括受试小鼠外周血象和血清等23项生化指标进行综合分析,科学合理地“降维”后,克服了多指标综合评价带来的统计和分析,筛选出与抗疲劳和耐缺氧功效最直接相关的主要功效指标,依据主要考核变量的综合评分最终确定受试样品的功效特性大小。可见,主成分分析法可以作为一种方便、快捷和准确的量化评价功能学特性的新方法。
本条目由以下用户参与贡献
Angle Roh,funwmy,Zfj3000,Zhoujinsong-zjs,Dan,Beifu,Yixi,Tears~,twq,裴老师,Vulture,连晓雾,Mis铭,丁金鹏,y桑,Tracy,wzh.评论(共53条)
当维数大于时..就要使变量少于个,也就是维数小于.. 故意保留??
不是故意保留,是编辑遗漏,已更正,谢谢你的建议!
步骤4中,Z为p维,b也是p维,m指的是取m个主特征向量,这样就可以得到m个主成分,每个主成分其实就是原向量与对应特征向量的内积
得出主成分如何与数据对上号?若有例题分析就好了,过程全懂,一到结果分析就晕
补充了个主成分分析法在啤酒风味评价分析中的应用 希望能用的上
第一次参与编辑,好像没想像的难,哈
感谢Beifu的精彩贡献
搂住您好!我现在正在用主成分分析方法,我不是这个专业的,只是自学了一点,我用他在SPSS处理后得到得数据怎么才能知道原数据哪些属于第一主成分,哪些属于第二主成分呢?谢谢您啦!看了很多书也不懂哦
搂住您好!我现在正在用主成分分析方法,我不是这个专业的,只是自学了一点,我用他在SPSS处理后得到得数据怎么才能知道原数据哪些属于第一主成分,哪些属于第二主成分呢?谢谢您啦!看了很多书也不懂哦
特征值按从大到小排,最大的是第一主成份,以此类推。
spss相关系数矩阵不正定对主成分分析影响?? 是否能用主成分分析法
是的,能用主城分析发的
spss给出的“成份矩阵”中,x7: 0.400 -0.235 0.343 -0.176 0.388 -0.269 其中,没有大于0.5的,怎么办?另外,没有最大的特征值负载在提取出来的最后一个主成分上,是那里出问题了,请不吝赐教。
主分是不是就是坐标轴?用pca的目的是降维,得到一个新的矩阵,这个新的矩阵是主成分的得分矩阵。。。。这么理解对吗?(嘻嘻。。。我是初学者。。。谢啦)
搂住您好!我现在正在用主成分分析方法,我不是这个专业的,只是自学了一点,我用他在SPSS处理后得到得数据怎么才能知道原数据哪些属于第一主成分,哪些属于第二主成分呢?谢谢您啦!看了很多书也不懂哦
你现在懂了吗,我现在也正开始看,和你一样的问题,帮我解释一下可以吗?
请问下主成分分析有哪些参考书?
你找参考书了吗,帮我推荐一下,谢谢啦~
添加了新内容,希望对您有帮助!
你好,请教一下主成分分析法需要有数据才能分析么?
?没有数据能分析啥呢?









受益匪浅