RAS法
出自 MBA智库百科(https://wiki.mbalib.com/)
RAS法——又名適時修正法、雙比例尺度法（Biproportional Scaling Method ）
目錄 |
RAS法是1960年同樣由英國著名經濟學家斯通等人發展起來的，在實際應用中不斷得到改進，現在已得到十分廣泛地普及。
所謂“RAS法”是指在已知計劃期（預測期）的某些控制數據的條件下，修正原有投入產出表直接消耗繫數矩陣，並據以編製計劃期投入產出表的一種方法。
RAS法是已知如下信息，估計目標年份投入產出表中間投入流量的演算法。
（1）基年投入產出表的中間投入矩陣與總產出。
（2）目標年各部門的總產出。
（3）目標年各部門的中間投入合計。
（4）目標年各部門的中間使用合計。
用目標年的各部門總產出乘以基年相應的投入結構，得到中間投入矩陣，如果其行合計不等於目標年的中間使用合計，或者列合計不等於目標年的中間投入合計，則對基年結構進行調整，調整後依據目標年的各部門總產出計算出的中間投入矩陣的行合計、列合計，應與目標年中間使用合計、目標年中間投入合計相同。
1.數據成本低。
2.數學性質優良，它有唯一解且快速收斂。
3.操作簡易。
4.可靠程度較高。
所謂“改進的RAS法”是指：在RAS法的基礎上，根據其所存在的問題，而提出的一種簡單的改進方法。亦即在原方法中對某些繫數（一般來說，是指那些變動特別大或特別小的繫數）可採用事先修訂（或確定不變）的數據，而其餘的繫數則用RAS法求得，即在具體計算過程中先從繫數矩陣中剔除這些已知的繫數，求解以後再加進去。
RAS法的計算[1]
下麵將通過一個具體的例子，來介紹RAS法的具體計算過程。
例子：已知條件：
已知報告期投入產出表的直接消耗繫數矩陣為：
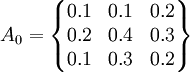
已知計劃期（預測期）各部門的總產出向量、最終產品向量、凈產值向量分別為：
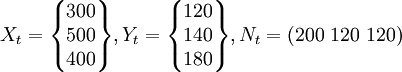
根據條件2），在抽象掉固定資產運動的情況下，可以計算出計劃期各部門物資消耗的合計數和中間產品的合計數，即:
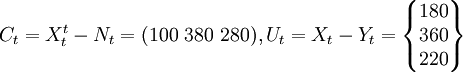
由此，假設條件已滿足了R·A·S法的基本條件，可以具體進行了。“R”的含義是“行乘數”，而“S”的含義是“列乘數”。因此，R·A·S法的基本思路就是，計算出“行乘數”和“列乘數”，然後用它們來不斷調整報告期的直接消耗繫數矩陣，直到滿意的結果為止。
下麵是具體的計算和調整過程：
從上述計算過程中可以得到總的“行乘數”R和“列乘數”S：
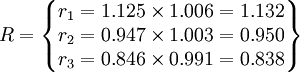
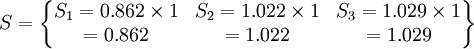
由此我們有:
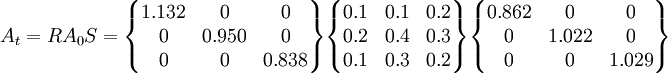
同時，我們還可得到計劃期投入產出表的流量表計算過程：
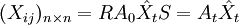
其中，
是計劃期各部門總產量的對角矩陣（同時註意：對角矩陣相乘時可以變換位置，而不會影響計算結果）。
- ↑ 中國人民大學公共管理學院精品課程《投入產出分析》 第五章 投入產出表的編製方法 第六節 直接消耗繫數的修正與預測
