價格斷裂點模型
出自 MBA智库百科(https://wiki.mbalib.com/)
價格斷裂點模型(Gabor Granger)
目錄 |
價格斷裂點模型(Gabor Granger)是由Gabor和Granger在1965年提出的,對於新產品預先確定好幾個可能的價格,然後對每一價格詢問被訪者購買產品的可能性,由此可以確定產品的最優價格以及分析產品價格變化對需求的影響。
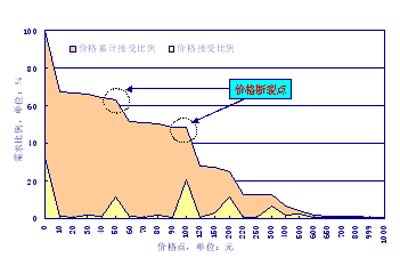
圖:價格斷裂點模型
這種價格研究方法是預先確定好產品或服務的幾個可能的價格,通過訪問詢問被訪者每一可能價格的購買可能性(購買可能性通常用5分制來表示,5分代表非常可能,1分代表非常不可能);
然後計算出不同價格點下非常可能購買的百分比,繪製價格需求曲線,並據之進行分析,找到價格斷裂點,該價格點附近的微小變動會帶來購買興趣的明顯下降,即可以此價格點作為市場參考價。
價格斷裂點模型運用案例[1]
首先讓客戶充分瞭解產品情況,一般是由銷售員給客戶介紹樓盤的情況,並讓客戶看到園林和樣板房(如果沒有看模型也可以),然後開始詢問客戶,當售價分別為P1、P2、P3、P4或P5,他購買的可能性分別是多大。
一般這些價格都是與市場價格比較接近的,價格都會從低到高來排序,一般的結果是價格越低越傾向於購買,價格越高越傾向於不購買,如果結果正好相反,這是有邏輯上的問題的,這種類型問卷的數據我們可以不予採用。有的時候為了得到精確的價格需求關係,會設置10個以上的價格水平,雖然在理論上確實可以得到產品價格變化對需求的影響,但是在實際操作過程中是非常難以實現的,銷售員也不希望讓客戶花這麼多時間來回答這樣一個很傷腦筋的問題。
由於每一套單位的價格不盡相同,所以這種剔除每一套單位的特殊性來測試價格的做法並不是非常科學,一般來說可以將這個價格設定為均價,同時根據景觀、朝向等主要的差價因素來將產品分為幾類,讓客戶選擇了某一類產品之後再來做上面的調查。例如A項目是一個江景樓盤,其差價主要表現在景觀上,所以可以將所有單位分為有江景和非江景的單位,如果客戶喜歡江景單位,那就讓客戶針對江景價格來給出購買的可能性,如果客戶想買非江景單位,則讓客戶針對非江景給出購買的可能性。
得到以上的數據之後就模擬購買過程,將某一個價格水平下所有表示肯定或者可能會購買的比例算出來,並根據客戶總數量和比例來計算銷售套數,併進一步估計出銷售額,便得到了一個對應的關係,將其他幾個價格對應的銷售額都算出來,如果還對產品進行了分類,則需要分類來分別統計可能的銷售額,甚至還可以實現不同的組合。例如A項目,我們就分開江景均價和非江景均價,兩大類進行調查,得到了兩個不同的對應關係。
假設針對A項目的江景單位,通過調查得到以下結果:
| 價格水平(元) | 肯定或可能購買的百分比(%) | 銷售套數 | 估計銷售金額(萬元) |
|---|---|---|---|
| 6000 | 95.8 | 153 | 11036 |
| 7000 | 82 | 131 | 11021 |
| 8000 | 52.9 | 85 | 8125 |
| 9000 | 14.1 | 23 | 2436 |
| 10000 | 4.8 | 8 | 922 |
| 11000 | 2.1 | 3 | 444 |
| 12000 | 0.9 | 1 | 207 |
將上面的表圖成一個更直接的圖形,以銷售額為橫坐標,以價格為縱坐標,得到需求的價格曲線的示意圖,雖然並不是十分精確,但是基本上可以說明問題。
賣到8000元/平方米,在這個價格水平下估計可以賣到8125萬元,如果賣到9000元/平方米,則銷售額就會減至2436萬元,如果再高一點賣到10000元/平方米,則銷售額只有922萬元。有幾點我們也需要註意:
1、調研中有一個客戶數量的基礎數據,本例使用了認籌客戶數量這個值,在實際操作過程中,這個數字會不斷變化,而且受到廣告投放等因素的影響較大,需要靈活對待;
2、由於房地產相對其他產品本身的價格的敏感度就是偏低的,兩套房子之間差幾千甚至上萬塊錢可能對客戶的購買都不會產生決定性的影響,所以一般來說調查得到的價格還能夠有5%左右的浮動範圍,也就是說能夠接受8000元/平方米的客戶可能大多數也能夠接受8400元/平方米的價格;
3、6000到7000元/平方米,還有10000到12000元/平方米是兩個非彈性需求的價格區間,對價格敏感度不高,而8000到9000是一個彈性需求區域,對價格相對更敏感;
4、因為A項目開盤時,對項目的價格把握不大,所以本例所劃分的價格區間較大,接下來可以再縮小範圍,細分區間,建議價格差額不要小於5%,本例就可以500元/平方米為間隔。