CFLP法
出自 MBA智库百科(https://wiki.mbalib.com/)
CFLP法(Capacitated Facility Location Problem)
目錄 |
什麼是CFLP法[1]
CFLP法是反町洋一先生創造併發表的方法,即用LP(線性規劃)運輸法,確定各配送中心的市場占有率,求出配送分擔地區的重心,再用混合整數計劃法的“籌劃型”確定場址的建設位置。其目標函數和約束條件表示如下。
| minZ = | ∑ | ∑ | CijXij + | ∑ | FiYi |
| i | j | i |


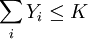
式中 N——需要地的個數;
M——配送中心建設候補地的個數;
K——建設配送中心的個數;
Dj——需要地(j)的需要量;
Fi——配送中心建設候補地(i)的不變建設費;
Ai——配送中心建設候補地的建設容量;
Cij——從候補地(i)到需要地(j)的運輸單價;
Xij——從配送中心到需要地(j)的運輸量;
Yi——假定在候補地(i)建設配送中心時為1,否則為0。
CFLP法的基本原理[2]
當配送中心的能力有限制,而且用戶的地址和需求量及設置多個配送中心的數目均已確定的情況下,可採用CFLP法(Capacitated Facility Location Problem),從配送中心的備選地點中選出總費用最小的由多個配送中心(假設有m個)組成的配送系統。這個方法的基本步驟如下。
首先,假定配送中心的備選地點已定,據此假定在保證總運輸費用最小的前提下,求出各暫定配送中心的供應範圍。然後,再在所求出的供應範圍內分別移動配送中心至其他備選地點,以使各供應範圍的總費用下降。當移動每個配送中心的地點都不能繼續使本區域總費用下降時,則計算結束;否則,按可使費用下降的新地點,再求各暫定配送中心的供應範圍,重覆以上過程,直到費用不再下降為止。
(1)初選配送中心的地點。通過定性分析,根據配送中心的配送能力和用戶需求分佈情況適當地確定配送中心的數量及其設置地點,並以此作為初始方案。這一步驟非常重要,因為它將直接影響整個計算的收斂速度。
(2)確定各暫定的配送中心的供應範圍。設暫定的配送中心有k個,分別為s1,s2,…,sk;用戶有n個;從配送中心si到用戶j地的單位運輸費用為 ;以運輸費用U最低為目標,則可構成的運輸問題模型如下:
;以運輸費用U最低為目標,則可構成的運輸問題模型如下:
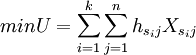



式中: ——配送中心si到用戶j的運輸量;
——配送中心si到用戶j的運輸量;
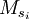 ——配送中心si的容量;
——配送中心si的容量;
Dj——用戶j的需求量。
解以上運輸問題,就可求得各暫定配送中心的供應範圍。這可表述為如下的用戶集合:


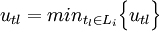
若 ,說明步驟(3)求出的目標函數值是步驟(2)求出的第i個配送中心目標函數值的一部分,則令si'=ti';否則令si'=si。對所有k個區域重覆上述過程,得到新的配送中心的集合
,說明步驟(3)求出的目標函數值是步驟(2)求出的第i個配送中心目標函數值的一部分,則令si'=ti';否則令si'=si。對所有k個區域重覆上述過程,得到新的配送中心的集合 。
。
(4)比較新、舊配送中心集合的總費用。若前者大於或等於後者,說明已經得到了所要求的解,計算可停止;若前者小於後者,說明新得到的配送心地點可使總費用下降,通過改善配送中心的供應範圍,還有可能進一步降低總費用。為了進一步降低總費用,以新的配送系統代替原有的配送系統,重覆步驟(2)至步驟(4),直到總費用不能再下降為止。
按以上步驟得到的收斂解,雖然沒有得到理論上的證明,但是由於費用總是在下降的,因此在實際應用中,可以充分相信所得到的解。
案例一:[2]

解:根據圖1可得各需求點之間的最短運輸距離如表1所示。
表1 各需求點之間的最短運輸距離
| 需求點j\需求點i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | O | 1 | 6 | 7 | 4 | 3 | 4 | 6 | 6 | 9 | 8 | 9 |
| 2 | 1 | 0 | 5 | 6 | 5 | 4 | 5 | 7 | 7 | 10 | 9 | 10 |
| 3 | 6 | 5 | 0 | 3 | 6 | 9 | 10 | 12 | 12 | 15 | 14 | 15 |
| 4 | 7 | 6 | 3 | O | 3 | 10 | 11 | 13 | 13 | 16 | 15 | 12 |
| 5 | 4 | 5 | 6 | 3 | 0 | 7 | 8 | 10 | 10 | 13 | 12 | 9 |
| 6 | 3 | 4 | 9 | 10 | 7 | 0 | 6 | 4 | 9 | 10 | 6 | 6 |
| 7 | 4 | 5 | 10 | 1l | 8 | 6 | O | 2 | 9 | 5 | 4 | 9 |
| 8 | 6 | 7 | 12 | 13 | 10 | 4 | 2 | 0 | 10 | 6 | 2 | 7 |
| 9 | 6 | 7 | 12 | 13 | 10 | 9 | 9 | 10 | O | 4 | 8 | 13 |
| 10 | 9 | 10 | 15 | 16 | 13 | 10 | 5 | 6 | 4 | O | 4 | 9 |
| 11 | 8 | 9 | 14 | 15 | 12 | 6 | 4 | 2 | 8 | 4 | O | 5 |
| 12 | 9 | 10 | 15 | 12 | 9 | 6 | 9 | 7 | 13 | 9 | 5 | 0 |
(1)根據需求量的分佈情況,可將配送中心的初始位置暫定在4、6、9三個節點上。
(2)以點4、6、9為配送點,其他各節點為需求點,求運輸問題的最優解,如表3一12所示。於是得到初始方案,總費用為179個單位。(具體求解過程略)
(3)根據以上求得的初始解,可以看出配送中心4的配送範圍為用戶1、2、3、4、5的集合,配送中心6的配送範圍為用戶1、6、8、12的集合,配送中心9的配送範圍為用戶1、7、9、10、11的集合。
表2 配送中心佈局的初始方案
| 配送中心\需求點 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 供應量 |
| 4 | 2 | 4 | 2 | 3 | 2 | 13 | |||||||
| 6 | 2 | 4 | 5 | 2 | 13 | ||||||||
| 9 | 1 | 3 | 4 | 3 | 2 | 13 | |||||||
| 需求量 | 5 | 4 | 2 | 3 | 2 | 4 | 3 | 5 | 4 | 3 | 2 | 2 | 39 |
對於集合{1,2,3,4,5},配送中心的位置設在4時配送費用為:

如果配送中心的位置從4移到其他需求點,則配送費用分別為:
如果移到1,則 ;
;
如果移到2,則 ;
;
如果移到3,則 ;
;
如果移到5,則 。
。
所以,移到配送中心2時,配送費用最少。
同理,通過計算,可知對於用戶集合{l,6,8,12},配送中心移到6,配送費用最小;對於用戶集合{1,7,9,10,11},配送中心移到10,配送費用最小。於是,新的配送系統應由用戶集合{2、6、10}組成。
(4)對新的配送系統{2,6,10}重覆步驟(2)至步驟(4),重新計算。經計算,再次計算所得配送中心方案與前一次結果相同,說明方案已達到最優,所以最終解決方案就是配送中心選擇在{2,6,10},供應方案如表3所示,總費用為152個單位。
表3 配送中心佈局的最終方案
| 配送中心\需求點 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 供應量 |
| 2 | 2 | 4 | 2 | 3 | 2 | 13 | |||||||
| 6 | 3 | 4 | 4 | 2 | 13 | ||||||||
| 10 | 3 | 1 | 4 | 3 | 2 | 13 | |||||||
| 需求量 | 5 | 4 | 2 | 3 | 2 | 4 | 3 | 5 | 4 | 3 | 2 | 2 | 39 |
CFLP法的前半部分屬於線性規劃運輸問題的解法,但其又在後半部分對線性規划進行了進一步的完善。雖然該方法實際意義明顯,但缺乏理論上的證明。







