隨機博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
隨機博弈(Stochastic Games)
目錄 |
在博弈論中，隨機博弈是一類由一個或多個參與者進行的、具有狀態概率轉移的動態博弈，是由勞埃德·夏普利（Lloyd Shapley）於20世紀50年代初期提出。
隨機博弈由一系列階段組成。在博弈中每一階段的起始，博弈處於某種特定狀態。每一參與者選擇某種行動，然後會獲得取決於當前狀態和所選擇行動的收益。之後，博弈發展到下一階段，處於一個新的隨機狀態，這一隨機狀態的分佈取決於先前狀態和各位參與者選擇的行動。在新狀態中重覆上述過程，然後博弈繼續進行有限或無限個數的階段。一個參與者得到的總收益常用各階段收益的貼現和，或是各階段收益平均值的下限來計算。
隨機博弈是指的是這樣的一個博弈游戲，目前有任意堆石子，每堆石子個數也是任意的，雙方輪流從中取出石子，規則如下：
1、每一步應取走至少一枚石子；每一步只能從某一堆中取走部分或全部石子。
2、如果誰取到最後一枚石子就勝。
隨機博弈的組成部分有：有限參與者集I ；狀態空間M （可以是有限集，也可以是可測空間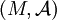
）；對於每一參與者
，存在行動集
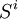（可以是有限集，也可以是可測空間
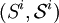）；P 是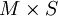
到M 的轉移概率，其中
是行動組合，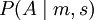
是下一狀態處於A 中的概率，而A 給定了當前狀態m 和當前行動組合s ；從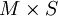到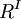
的收益函數g，其中g 的第i 個坐標
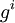是參與者i 的收益，而 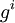是狀態m 和行動組合s 的函數。
博弈以某個初始狀態m1 開始。在階段t 中，參與者最先觀測到mt ，同時選擇行動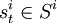
，然後觀測到行動組合
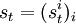，然後以概率
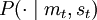自然選擇mt + 1 。一次隨機博弈
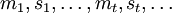定義了一個收益流
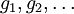，其中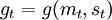
。
隨機博弈由多個博弈階段組成。在每一個階段的開始，博弈處在某個特定狀態下。參與者選擇自身的策略並獲得相應的由當前狀態和策略決定的報酬。然後博弈按照概率的分佈和參與者策略隨機轉移到下一個階段。在新的狀態階段，重覆上一次的策略選擇過程，然後博弈繼續進行。參與者在隨機博弈中獲得的全部報酬一般用各個階段報酬的貼現值來計算，或者用各個階段報酬平均值的下限來計算。
如果隨機博弈中參與者的數量有限並且每個博弈階段可能的狀態數量有限，那麼一個具有有限博弈階段的隨機博弈一般都存在一個納什均衡。同樣的，對於一個具有無窮階段的隨機博弈，如果使用各個階段報酬的貼現值來計算整個博弈階段的報酬，那麼這個隨機博弈也是具有納什均衡的。尼古拉斯·維勒（Nicolas Vieille）已經證明具有有限階段和有限狀態的兩人隨機博弈當中，如果博弈過程的報酬使用各個階段報酬平均值的下限來計算的話，是具有逼近納什均衡的。然而，包含2個以上的參與者的隨機博弈是否存在納什均衡，仍然是個未決的問題。
貼現因數為λ（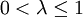
）的貼現博弈Γλ 中，參與者i 的收益是
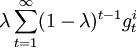。n 階段博弈中，參與者i 的收益是
。
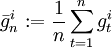若存在有限多個狀態和行動的二人零和博弈Γn（各自是Γλ）的值為vn(m1)（各自是vλ(m1)），則vn(m1) 在n 趨於無窮時收斂到一個極限，且vλ(m1)在λ趨於0時收斂到相同的極限。這一結論已被杜魯門·彪利（Truman Bewley）和艾朗·克爾伯格（Elon Kohlberg）於1976年證明。[1]
非貼現博弈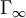
中，參與者i 的收益是各階段收益平均值的極限。在定義二人零和博弈
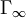的值與非零和博弈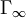的均衡收益之前需要註意一些事情：若對於每一
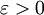都有正整數N 、參與者1的策略
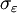和參與者2的策略
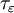，二人零和隨機博弈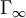的一致值（uniform value）
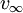存在，這樣對於每一σ、τ和每一
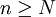，博弈中由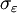和τ定義的概率的
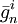期望至少為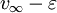
，由σ和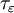定義的概率的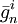期望至多為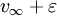
。讓·弗朗索瓦·梅頓斯（Jean Francois Mertens）和亞伯拉罕·奈曼（Abraham Neyman）於1981年證明二人零和隨機博弈具有一致值。[2]
若參與者數量有限且行動集和狀態集有限，則有限階段隨機博弈總有納什均衡，對於總收益是貼現和的無限多階段隨機博弈也是如此。尼古拉斯·維勒（Nicolas Vieille）已經證明當總收益是各階段收益平均值的下極限時，所有具有有限狀態和行動空間的二人隨機博弈都有近似納什均衡。不過，當參與者多於2名時，隨機博弈是否存在這類均衡仍是一個極具挑戰性的開放性問題。[3]
隨機博弈在經濟學、演化生物學和電腦網路中都有應用。事實上，隨機博弈是重覆博弈的一般化過程（重覆博弈是指在每個博弈階段都處於相同的狀態）。
亞伯拉罕·奈曼（Abraham Neyman）和Sylvain Sorin所著的書籍是最完備的有關隨機博弈的參考材料。Jerzy A. Filar和Koos Vrieze所著的書更為基礎[1]，在書中給出了嚴密的關於[[馬爾可夫決策過程]（MDP）和雙人隨機博弈的標準處理方法。他們創造了Competitive MDPs這個術語來概括單人和雙人隨機博弈這個概念[4]。
- ↑ 1.0 1.1 Abraham Neyman，Sylvain Sorin. Stochastic Games and Applications. Kluwer Academic Press. 2003年10月31日. ISBN 978-1402014932 （英文）
- ↑ Jean Francois Mertens，Abraham Neyman. Stochastic Games. International Journal of Game Theory. June 1981, 10 (2): 第53－66頁.
- ↑ Nicolas Vieille. Stochastic games: Recent results //R.J. Aumann，S. Hart. Handbook of Game Theory with Economic Applications
- ↑ Jerzy A. Filar，Koos Vrieze. Competitive Markov Decision Processes. Springer-Verlag. 1996年11月15日. ISBN 978-0387948058 （英文）
