約翰遜法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是約翰遜法?[1]
約翰遜法是作業排序中的一種排序方法。選出最短加工時間i*,若最短加工時間有多個,任選1個.若i*出現在機床1,它對應的工件先安排加工,否則放在最後安排,安排後划去該工件,重覆上兩個步驟,直到所有工件都排序完畢。
約翰遜法適用的條件是:n個工件經過二、三台設備(有限台設備)加工,所有工件在有限設備上加工的次序相同。
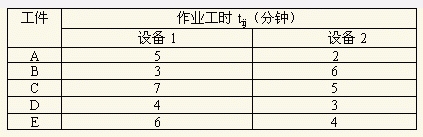
舉例說明:有五個工件在二台設備上加工,加工順序相同,現在設備1上加工,再在設備2上加工,工時列於下表1中,用約翰遜法排序。
表1 加工工時表
約翰遜法具體步驟[1]
第一步,取出最小工時t12=2。如該工時為第一工序的,則最先加工;反之,則放在最後加工。此例是A工件第二工序時間,按規則排在最後加工。
第二步,將該已排序工作划去。
第三步,對餘下的工作重覆上述排序步驟,直至完畢。此時t21=t42=3,B工件第一工序時間最短,最先加工;D工件第二工序時間最短,排在餘下的工件中最後加工。最後得到的排序為:B-C-E-D-A。整批工件的停留時間為27分鐘。
約翰遜法實例分析[2]
這是一種適用於n/2/P/Fmax排序問題的靜態排序方法約翰遜法的目標是要求得到全組的零件具有最短的生產周期的生產進度表。數學上可以證明,應用約翰遜法所得的排序結果是最優解。
1.約翰遜法的排列規則
如果滿足mint1k;t2k < mint2k;t1k
則將k工件排在h工件之前。
式中:t1k、t2k:k工件第1工序、第2工序的加工時間;
t2k、t1k:h工件第2工序、第1工序的加工時間。
2.約翰遜排序法的進行步驟
(1)列出零件組的工序矩陣;
(2)在工序矩陣中選出加工時間最短的工序。如果改工序屬於第1工序,則將該工序所屬工件排在前面。反之,最小工序是第2工序,則將該工序所屬的工件排在最後面。若最小的工序又多個,可任選其中的一個;
(3)將已排序的工件從工序矩陣中消去;
(4)繼續按步驟(1)、(2)、(3)進行排序,若所有工件都已排定投產順序,排序即告結束。
例:有6中零件,其工序矩陣見表
表:零件的工序矩陣
| 工件號 | 1 | 2 | 3 | 4 | 5 | 6 |
| 第1工序M1 | 6 | 2 | 9 | 4 | 4 | 5 |
| 第2工序M2 | 8 | 3 | 3 | 5 | 8 | 4 |
根據約翰遜法的排序步驟:
(1)按前工序最小的選出2號工件及後工序最小的選出3號工件前,3號排在後。從原工件矩陣中消去2號及3號零件,見下表。
| 項目 | 新工序矩陣 | 原工序矩陣 | ||||
| 工件號 | 2 | 3 | 1 | 4 | 5 | 5 |
| 第1工序M1 | 2 | 9 | 6 | 4 | 4 | 5 |
| 第2工序M2 | 3 | 3 | 8 | 5 | 8 | 4 |
(2)對原工件矩陣繼續步驟(1)、(2)、(3),前工序最小的有4和5號兩工件可任選其一,後工序最小的為6號工件。選出該兩工件,並按前述規則排列,插入新工序矩陣見下表。
| 項目 | 新工序矩陣 | 原工序矩陣 | |||||
| 工件號 | 2 | 4 | 6 | 3 | 1 | 5 | |
| 第1工序M1 | 2 | 4 | 5 | 9 | 6 | 4 | |
| 第2工序M2 | 3 | 5 | 4 | 3 | 8 | 8 | |
(3)按規則繼續進行排序,5號工件排在前,1號工件拍在後。
工序矩陣。表是按約翰遜法排序後的新工藝矩陣。
按約翰遜法排序後的新工藝矩陣
| 項目 | 新工序矩陣 | |||||
| 工件號 | 2 | 4 | 5 | 1 | 6 | 3 |
| 第1工序M1 | 2 | 4 | 6 | 5 | 9 | |
| 第2工序M2 | 3 | 5 | 8 | 8 | 4 | 3 |
對於同順序排序問題,可以通過表上作業,計算全組零件的最大流程時間Fmax見表
最大流程時間Fmax計算表
| 工件號 | 2 | 5 | 4 | 1 | 6 | 3 |
| 第1工序M1 | 2/2 | 4/6 | 4/10 | 6/16 | 5/21 | 9/30 |
| 第2工序M2 | 3/5 | 5/11 | 8/19 | 8/27 | 4/31 | 3/34 |
表中斜線右方的數字是到該工序結束時的流程時間,它的計算方法如下:
到該工序結束時間的流程時間=該工序的開始時間+該工序的加工時間
在生產過程中一個工序的開始時間取決於兩個因素:
- 該工序前一道工序的結束時間;
- 該工序所用的設備上緊前工件的加工結束時間。該工序的開始時間應取上述兩數中之大者。例如,1號工件第2工件結束時的流程時間,應為Fj1m2=max{16;19}+8=27。
根據上表中的數據可得到一張1至6號工件的生產進度表,有每個工件在各台設備上的開工時間與完工時間。
本例中第4和第5號工件在被選時,由於前工序均為最小工序,當時任選了4號。如果選了5號結果有如何呢?見下表。
本例不同排序方案的最大流程計算
| 工件號 | 2 | 5 | 4 | 1 | 6 | 3 |
| 第1工序M1 | 2/2 | 4/6 | 4/10 | 6/16 | 5/21 | 9/30 |
| 第2工序M2 | 3/5 | 8/14 | 5/19 | 8/27 | 4/31 | 3/34 |
根據上面兩表的計算結果,說明對於條件等價的條件,任選其中之一,不影響最後結果。按約翰遜法所排出的結果應為最優解,這裡說明最優解可能不止一個,可以有多個等值的最優解。
約翰遜法只適用於兩工序工件的排序問題,所以它的使用範圍受到很大的限制。








懂了,看書看不懂,倒是例子很好,明白了謝謝。