等可能事件

出自 MBA智库百科(https://wiki.mbalib.com/)

　　等可能事件是指每個基本事件出現的可能性都相等．若某一試驗由n個基本事件組成（即等可能出現n個結果，則每個基本事件的概率是），如果某個事件A包含的結果有m個（既包含有m個基本事件），那麼事件A的概率為．

　　註意：是等可能事件概率的定義，同時也是計算這種概率的一種方法．利用這個式子計算概率時，關鍵是求出m、m，n為一次試驗中等可能出現的結果數，m為某個事件A所包含的結果數．求n時，應註意這幾種結果必須是等可能的．

　　【舉例】：先後拋擲兩枚質地均勻的硬幣，求“一枚出現正面，另一枚出現反面”的概率．

　　分析：先後拋擲2枚質地均勻的硬幣，可出現“正，正”、“正，反”、“反，正”、“反，反”這4種等可能的結果．而“一枚出現正面，另一枚出現反面”這一事件包括“正，反”、“反，正”兩種結果．

　　解：設一枚出現正面，另一枚出現反面的事件為A，則

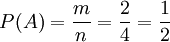
　　∴“一枚出現正面，另一枚出現反面”的概率為．

　　註意：解答本題，有時錯誤認為先後拋擲2枚質地均勻的硬幣，只會出現“2個正面”、“2個反面”、“1正1反”這3種情況，從而得出 的結論．實際上述3種情況不是等可能的．

　　“互斥事件”和“等可能事件”是意義不同的兩個概念．在一次試驗中，由於某種對稱性條件，使得若幹個隨機事件中每一事件產生的可能性是完全相同的，則稱這些事件為等可能事件，在數目上，它可為2個或多個，而互斥事件是指不可能同時發生的兩個或多個事件．

　　兩種事件不是水火不相溶．有些等可能事件可能也是互斥事件，有些互斥事件也可能是等可能事件．

　　下麵通過舉例來辨清“互斥事件”和“等可能事件”．

　　【舉例1】 判斷以下各組中的事件是否是互斥事件？是否是等可能事件？

　　（1）粉筆盒裡有8支紅粉筆，6支綠粉筆，4支黃粉筆，現從中任取1支，“抽得紅粉筆”，“抽得綠粉筆”、“抽得黃粉筆”．

　　（2）李明從分別標有1，2，…，10標號的同樣的小球中，任取一球，“取得1號球”，“取得2號球”，…，“取得10號球”．

　　（3）一周七天中，“周一晴天”，“周二晴天”，…，“周六晴天”，“星期天晴天”

　　解：（1）“抽得紅粉筆”，“抽得綠粉筆”，“抽得黃粉筆”，它們是彼互斥事件，不是等可能事件．

　　（2）“取得1號球”，“取得2號球”，…，“取得10號球”，它們既是彼此互斥事件，又是等可能事件．

　　（3）“周一晴天”，…，“星期天晴天”，它們是等可能事件，不是彼此互斥事件．

　　【舉例2】 拋擲一均勻的正方體玩具（各面分別標有數1，2，3，4，5，6），事件A表示“朝上一面的數是奇數”，事件B表示“朝上一面的數不超過3”，求P(A＋B)．

　　下麵給出兩種不同解法

　　解法1：

　　∵，

　　∴

　　解法2：A＋B這一事件包括4種結果：即出現1，2，3和5。所以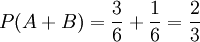

　　請你判明解法1和解法2的正誤．

　　解法1是錯誤的，解法2是正確的．

　　錯解的原因在於忽視了“事件和”概率公式應用的前提條件．由於“朝上一面的數是奇數”與“朝上一面的數不超過3”二者不是互斥事件．即出現1或3時，事件A、B同時發生，所以不能應用P(A+B)=P(A)+P(B)求解．

　　而解法2中，將A＋B分成出現“1，2，3”與“5”這兩個事件，記出現“1，2，3”為事件C，出現“5”為事件D，則C與D兩事件互斥

　　∴

　　∴解法2正確．