直送式配送運輸
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是直送式配送運輸[1]
直送式配送運輸是指由一個供應點對一個客戶專門送貨。從物流優化的角度看,直送式客戶的基本條件是其需求量接近於或大於可用車輛的額定載重量,需專門派一輛或多輛車一次或多次送貨。因此,直送情況下,貨物的配送追求的是多裝快運,選擇最短配送線路,以節約時間、費用,提高配送效率。即直送問題的物流優化,主要是尋找物流網路中的最短線路問題。
直送式配送運輸的方法[2]
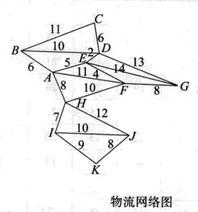
目前求解最短線路問題的方法很多,如位勢法、“帚”形法、動態法等。現以位勢法為例,介紹如何解決物流網路中的最短線路問題。已知物流網路如圖所示,各結點分別表示為A、B、C、D、E、F、I、J、K,各結點間的距離如圖所示,試確定各結點間的最短線路。
尋找最短線路的方法步驟如下:
第一步:選擇貨物供應點為初始結點,並取其位勢值為“零”即VI = 0;
第二步:考慮與I點直接相連的所有線路結點。設其初始結點的位勢值為VI,則其終止結點J的位勢值可按下式確定:
VJ = VI + LIJ
式中,LIJ為I點與J點之間的距離。
第三步:從所得到的所有位勢值中選出最小值,此值即為從初始結點到該點的最短距離,將其標在該結點旁的方框內,並用箭頭標出該連線IJ,以此表示從I點到J點的最短線路走法。如圖所示。
第四步:重覆以上步驟,直到物流網路中所有結點的位勢值均達到最小為止。
最終,各結點的位勢表示從初始結點到該點的最短距離。帶箭頭的各條連線則組成了從初始點到其餘結點的最短線路。分別以各點為初始結點,重覆上述步驟,即可得各結點之間的最短距離。
[例]在物流網路圖中,試尋找從供應點A到客戶K的最短線路。
解:根據以上步驟,計算如下:
(1)取VA = 0;
(2)確定與A點直接相連的所有結點的位勢值:
VB = VA + LAB = 0 + 6 = 6
VE = VA + LAE = 0 + 5 = 5
VF = VA + LAF = 0 + 11 = 11
VH = VA + LAH = 0 + 8 = 8
(3)從所得的所有位勢值中選擇最小值V_E=5,標註在對應結點E旁的方框內,同時用箭頭標出連線AE。即minVB,VE,VF,VH = min6,5,11,8 = VE = 5
(4)以E點為初始結點,計算與之直接相連的D,G,F點的位勢值。
VD = VE + LED = 5 + 2 = 7
VG = VE + LEG = 5 + 14 = 19
VF = VE + LEF = 5 + 4 = 9
(5)從所得的所有剩餘位勢值中選出最小值6,標註在對應的結點B旁,同時用箭頭標出連線AB。即
minVB,VH,VD,VG,VF = min6,8,7,19,9 = VB = 6
(6)以B點為初始結點,計算與之直接相連的D,C點的位勢值。
VD = VB + LBD = 6 + 10 = 16
VC = VB + LBC = 6 + 11 = 17
同一節點有多個位勢值,則只保留最小值,即取VD=7。
(7)從所得的所有剩餘位勢值中取最小值VD=7,標註在與之相應的D旁的方框內並用箭頭標出其連線ED。即
min8,7,19,9,17 = VD = 7
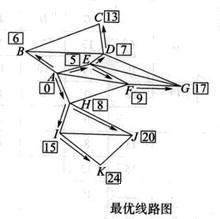
如此繼續計算,可得最優路線如圖所示,由供應點A到客戶K的最短距離為24。
依照上述方法,將物流網路中的每一個結點當做初始結點,並使其位勢值等於“零”,然後進行計算,可得所有結點之間的最短距離。如表所示。
| 物流網結點 | A | B | C | D | E | F | G | H | I | J | K |
| A | 0 | 6 | 13 | 7 | 5 | 9 | 17 | 8 | 15 | 20 | 24 |
| B | 6 | 0 | 11 | 10 | 11 | 15 | 23 | 14 | 21 | 26 | 30 |
| C | 13 | 11 | 0 | 6 | 8 | 12 | 19 | 21 | 28 | 33 | 37 |
| D | 7 | 10 | 6 | 0 | 2 | 6 | 13 | 15 | 22 | 27 | 31 |
| E | 5 | 11 | 8 | 2 | 0 | 4 | 12 | 13 | 20 | 25 | 29 |
| F | 9 | 15 | 12 | 6 | 4 | 0 | 8 | 10 | 17 | 22 | 26 |
| G | 17 | 23 | 19 | 13 | 12 | 8 | 0 | 15 | 22 | 27 | 31 |
| H | 8 | 14 | 21 | 15 | 13 | 10 | 15 | 0 | 7 | 12 | 16 |
| I | 15 | 21 | 28 | 22 | 20 | 17 | 22 | 7 | 0 | 10 | 9 |
| J | 20 | 26 | 33 | 27 | 25 | 22 | 27 | 12 | 10 | 0 | 8 |
| K | 24 | 30 | 37 | 31 | 29 | 26 | 31 | 16 | 9 | 8 | 0 |