直送式配送运输
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
什么是直送式配送运输[1]
直送式配送运输是指由一个供应点对一个客户专门送货。从物流优化的角度看,直送式客户的基本条件是其需求量接近于或大于可用车辆的额定载重量,需专门派一辆或多辆车一次或多次送货。因此,直送情况下,货物的配送追求的是多装快运,选择最短配送线路,以节约时间、费用,提高配送效率。即直送问题的物流优化,主要是寻找物流网络中的最短线路问题。
直送式配送运输的方法[2]
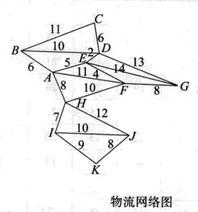
目前求解最短线路问题的方法很多,如位势法、“帚”形法、动态法等。现以位势法为例,介绍如何解决物流网络中的最短线路问题。已知物流网络如图所示,各结点分别表示为A、B、C、D、E、F、I、J、K,各结点间的距离如图所示,试确定各结点间的最短线路。
寻找最短线路的方法步骤如下:
第一步:选择货物供应点为初始结点,并取其位势值为“零”即VI = 0;
第二步:考虑与I点直接相连的所有线路结点。设其初始结点的位势值为VI,则其终止结点J的位势值可按下式确定:
VJ = VI + LIJ
式中,LIJ为I点与J点之间的距离。
第三步:从所得到的所有位势值中选出最小值,此值即为从初始结点到该点的最短距离,将其标在该结点旁的方框内,并用箭头标出该连线IJ,以此表示从I点到J点的最短线路走法。如图所示。
第四步:重复以上步骤,直到物流网络中所有结点的位势值均达到最小为止。
最终,各结点的位势表示从初始结点到该点的最短距离。带箭头的各条连线则组成了从初始点到其余结点的最短线路。分别以各点为初始结点,重复上述步骤,即可得各结点之间的最短距离。
[例]在物流网络图中,试寻找从供应点A到客户K的最短线路。
解:根据以上步骤,计算如下:
(1)取VA = 0;
(2)确定与A点直接相连的所有结点的位势值:
VB = VA + LAB = 0 + 6 = 6
VE = VA + LAE = 0 + 5 = 5
VF = VA + LAF = 0 + 11 = 11
VH = VA + LAH = 0 + 8 = 8
(3)从所得的所有位势值中选择最小值V_E=5,标注在对应结点E旁的方框内,同时用箭头标出连线AE。即minVB,VE,VF,VH = min6,5,11,8 = VE = 5
(4)以E点为初始结点,计算与之直接相连的D,G,F点的位势值。
VD = VE + LED = 5 + 2 = 7
VG = VE + LEG = 5 + 14 = 19
VF = VE + LEF = 5 + 4 = 9
(5)从所得的所有剩余位势值中选出最小值6,标注在对应的结点B旁,同时用箭头标出连线AB。即
minVB,VH,VD,VG,VF = min6,8,7,19,9 = VB = 6
(6)以B点为初始结点,计算与之直接相连的D,C点的位势值。
VD = VB + LBD = 6 + 10 = 16
VC = VB + LBC = 6 + 11 = 17
同一节点有多个位势值,则只保留最小值,即取VD=7。
(7)从所得的所有剩余位势值中取最小值VD=7,标注在与之相应的D旁的方框内并用箭头标出其连线ED。即
min8,7,19,9,17 = VD = 7
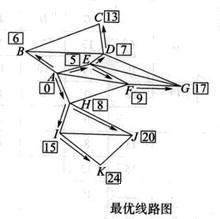
如此继续计算,可得最优路线如图所示,由供应点A到客户K的最短距离为24。
依照上述方法,将物流网络中的每一个结点当做初始结点,并使其位势值等于“零”,然后进行计算,可得所有结点之间的最短距离。如表所示。
| 物流网结点 | A | B | C | D | E | F | G | H | I | J | K |
| A | 0 | 6 | 13 | 7 | 5 | 9 | 17 | 8 | 15 | 20 | 24 |
| B | 6 | 0 | 11 | 10 | 11 | 15 | 23 | 14 | 21 | 26 | 30 |
| C | 13 | 11 | 0 | 6 | 8 | 12 | 19 | 21 | 28 | 33 | 37 |
| D | 7 | 10 | 6 | 0 | 2 | 6 | 13 | 15 | 22 | 27 | 31 |
| E | 5 | 11 | 8 | 2 | 0 | 4 | 12 | 13 | 20 | 25 | 29 |
| F | 9 | 15 | 12 | 6 | 4 | 0 | 8 | 10 | 17 | 22 | 26 |
| G | 17 | 23 | 19 | 13 | 12 | 8 | 0 | 15 | 22 | 27 | 31 |
| H | 8 | 14 | 21 | 15 | 13 | 10 | 15 | 0 | 7 | 12 | 16 |
| I | 15 | 21 | 28 | 22 | 20 | 17 | 22 | 7 | 0 | 10 | 9 |
| J | 20 | 26 | 33 | 27 | 25 | 22 | 27 | 12 | 10 | 0 | 8 |
| K | 24 | 30 | 37 | 31 | 29 | 26 | 31 | 16 | 9 | 8 | 0 |