灰色系統預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
灰色系統預測法是指對一些行為效果已知、而產生行為的原因較模糊的抽象灰色系統的預測方法。所謂灰色系統是介於白色系統和黑箱系統之間的過渡系統,一般地說,社會系統、經濟系統、生態系統都是灰色系統。
灰色系統預測主要包括:
1.數列預測,即對系統行為特征值的預測。
2.激勵預測,即對在一些突然性因素影響下的行為特征值的預測。
3.突變預測,即對系統的行為特征值超過一定限度而造成“突變”的時間的預測。
4.季節突變預測,即在某一特定時期內發生的突變的預測。
5.拓展預測,是對不規則波動系統的行為特征的波形的預測。
6.系統預測,是一種綜合預測,即先用不同模型表示變數之間的關係,得到一組模型,然後再進一步採用模型來表示諸模型組之間的關係,得到一個複合模型來進行預測。
該預測方法具有以下特點:
- 不需要大量的樣本;
- 預測精度較高;
- 用累加生成擬合微分方程,符合能量系統的變化規律;
- 可以進行長期預測。
(1)數據處理。假設給定原始時間數據序列為:
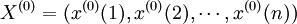 (4-40)
(4-40)
這些數據表現為:量少、無規律、隨機性強、波動明顯等。此時,將原始數據列進行一次累加生成1-AGO,獲得新的數據列:
 (4-41)
(4-41)
式中,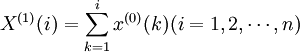 。由於新生成的數據列為一條單調增長的曲線,增加了原始數據列的規律性,弱化了其波動性。
。由於新生成的數據列為一條單調增長的曲線,增加了原始數據列的規律性,弱化了其波動性。
(2)建立微分方程。灰色系統建模思想是直接將時間序列轉化為微分方程,從而建立抽象系統的發展變化動態模型,簡記為GM。GM(1,1)模型的原始形式為:x(0)(k) + ax(1)(k) = b,其中,G表示Grey,M表示Model,1表示1階方程,1表示1個變數,a和b為參數。設
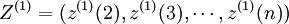 (4-42)
(4-42)
式中,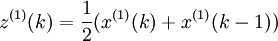 ,則稱
,則稱
x(0)(k) + az(1)(k) = b (4-43)
為GM(1,1)模型的基本形式。
若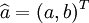 為參數列,且
為參數列,且
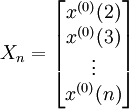 ,
,
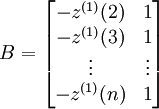 (4-44)
(4-44)
則灰色微分方程式(4-44)的最小二乘估計參數列滿足:
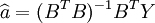 (4-45)
(4-45)
設非負序列X(0)和1-AGO序列X(1)如式(4-41)和式(4-42)所示,其中Z(1)為X(1)的緊鄰均值生成序列,如式(4-43)所示,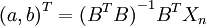 ,
,
則稱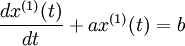 (4-46)
(4-46)
為灰色微分方程式(4-44)的白化方程,也叫影響方程。進行物流預測時,常常採用該白化方程。
(3)參數估計a和b。具體公式為式(4-45)和式(4-46),其中式(4-45)結合式(4-43)代入得
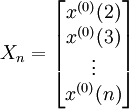 ,
,
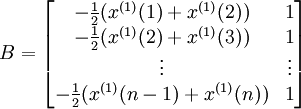 (4-47)
(4-47)
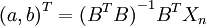 (4-48)
(4-48)
把式(4-47)代入式(4-48)可得a和b的值。
(4)預測模型。白化方程式(4-46)的解也稱時間相應預測值,具體為:
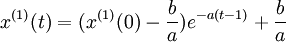 (4-49)
(4-49)
GM(1,1)灰色微分方程式(4-43)或式(4-46)的時間相應序列為:
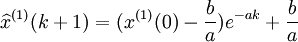 ,
,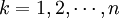 (4-50)
(4-50)
取x(1)(0) = x(0)(1),則
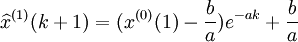 ,
,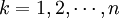 (4-51)
(4-51)
(5)還原模型。最後由於灰色系統理論建立的是累加數據的模型,因此我們必須對累加的數據進行還原,得到還原模型:
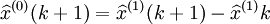 ,
,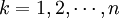 (4-52)
(4-52)
GM(1,1)模型的綜合預測模型為:
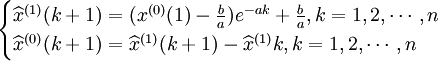
設原始序列為式(4-41),相應的預測模型序列為:
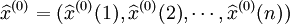
殘差序列為:
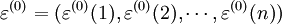
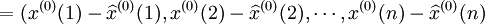
(1)殘差檢驗。按預測模型計算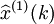 ,並將
,並將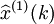 累減生成
累減生成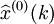 ,然後計算原始數據x(0)(k)與預測值
,然後計算原始數據x(0)(k)與預測值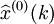 的絕對誤差序列和相對誤差序列:
的絕對誤差序列和相對誤差序列:
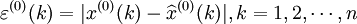 (4-53)
(4-53)
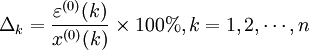 (4-54)
(4-54)
對於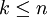 ,稱
,稱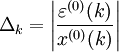 為k點模擬相對誤差,稱
為k點模擬相對誤差,稱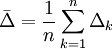 為平均相對誤差;稱
為平均相對誤差;稱 為平均相對精度,1 − Δk為k點的模擬精度
為平均相對精度,1 − Δk為k點的模擬精度 。給定α,當Δ < α且Δk < α成立時,該模型為殘差合格模型。
。給定α,當Δ < α且Δk < α成立時,該模型為殘差合格模型。
(2)後驗差檢驗。第1後驗指標為方差比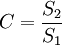 ,對於給定的C0 > 0,當C < C0時,稱模型為均方差合格模型。第2後驗指標為小誤差概率
,對於給定的C0 > 0,當C < C0時,稱模型為均方差合格模型。第2後驗指標為小誤差概率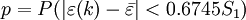 ,對於給定的p0 > 0,當p < p0時,稱模型為小誤差概率合格模型。
,對於給定的p0 > 0,當p < p0時,稱模型為小誤差概率合格模型。
上述式中:S1位原始序列標準差;S2為絕對誤差標準差;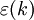 為預測誤差;
為預測誤差;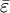 為其均值;p=m/n(m為小於上述條件的誤差個數)。通過檢驗的標準為精度等級月消越好,4級為不通過,精度等級如表4-8所示。
為其均值;p=m/n(m為小於上述條件的誤差個數)。通過檢驗的標準為精度等級月消越好,4級為不通過,精度等級如表4-8所示。
| 精度等級 | ||||
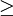 0.20 0.20
| ||||
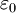 | 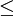 0.60 0.60
| |||
 0.70 0.70
| ||||
 0.65 0.65
| ||||
雖然GM(1,1)模型在預測方面應用廣泛且效果顯著,但並不是所有的數據序列都能建立GM(1,1)模型。在建立GM(1,1)模型之前,數列必須滿足一定的前提條件:
1)數據序列要滿足準光滑性條件,光滑比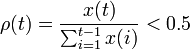 為準光滑性檢驗條件;
為準光滑性檢驗條件;
2)數據序列必須滿足灰指數規律,序列的變化速度不能太快,級比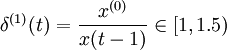 為準指數規律檢驗條件。
為準指數規律檢驗條件。
對於滿足準光滑性條件和灰指數規律的序列,可以建立GM(1,1)模型。一般非負系列累加生成後,可以得到光滑序列,非負光滑序列累加生成後,都會減少隨機性,呈現出近似的指數增長規律。原始數列越光滑,生成後的指數規律也越明顯。因此保證數列光滑性是生成指數的關鍵。對於非光滑或震蕩數列,一般經過二級弱化運算元作用後就能變成為光滑數列。







