派生存款乘數
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
[編輯]
什麼是派生存款乘數[1]
派生存款乘數：銀行存款貨幣創造機制所決定的存款貨幣的最大擴張倍數，稱為派生倍數。存款乘數是法定准備率的倒數。若以K表示存款總額變動對初始準備性存款變動的倍數，則：
K=1/法定准備金率
法定存款準備率越高，存款擴張倍數值越小；反之，擴張倍數值則越大。
[編輯]
制約派生存款乘數的因素還有：
（1）超額準備金制約；
（2）現金漏損的制約；
[編輯]
派生存款乘數實例分析[2]
多倍存款創造的總數是如何計算出來的?在這裡可以得到如下一個級數(沿用前例)：1000萬元，800萬元，640萬元，512萬元，409．60萬元等等。每個數字都是前一數字的80%(當然，20%的準備比率只是為舉例任意選擇的一個數字)，這樣一個序列構成一個等比級，按等比數列求和則有：
![AD=AR\cdot[1+(1-r_d)+(1-r_d)^2+(1-r_d)^3+\cdots]](/w/images/math/a/9/1/a916750826f9e11705b413733dd6f502.png)
即：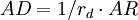
式中，AD表示經過派生的存款總額；AR表示中央銀行向商業銀行提供的初始準備金，或者說初始準備性存款的增額；rd表示法定存款準備率。
在上例中，在20%的準備比率條件下，存款創造總額為(1/20%)×1000萬元，即等於5000萬元。所以，這裡的存款乘數是5。銀行存款貨幣創造機制所決定的存款貨幣的最大擴張倍數，稱為派生倍數，即存款乘數。一般說來，它是法定准備率的倒數。
[編輯]
[編輯]
- ↑ 貨幣銀行學 模擬試題.西安電子科技大學網路與繼續教育學院
- ↑ 王秀芳,宋金傑,馬長海.貨幣銀行學.中國農業科學技術出版社,2003年08月第1版
一般說來，它是法定准備率的倒數。 問題就在於一般來說，誤導人。 我們關心的是，實際來說