正態分佈曲線
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自正态曲线)
正態分佈曲線(Normal distribution curve)，也稱鐘型曲線
目錄 |
[編輯]
什麼是正態分佈曲線[1]
正態分佈曲線反映了隨機變數的分佈規律。理論上的正態分佈曲線是一條中間高，兩端逐漸下降且完全對稱的鐘形曲線。
[編輯]
正態分佈曲線的特性[2]
正態分佈曲線具有以下幾個方面的主要特性。
1.正態分佈曲線是中間高、兩邊低、而且對稱的光滑曲線，曲線的最高瞄在平均數處，越是接近平均數的組，變數分佈的次數越多，離平均數越遠，分佈的次數越少。
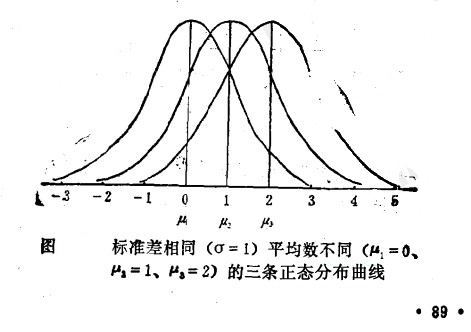
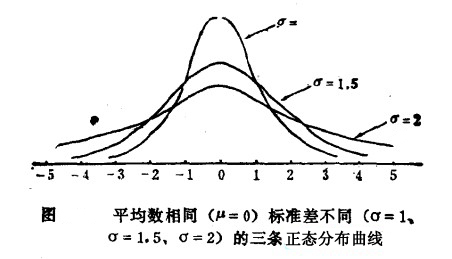
2.正態分佈曲線因總體平均數和標準差的不同呈現為不同的曲線，所以它不是一條曲線，而是一個曲線系統，不同的總體都有它自己的曲線。下兩圖表示平均數和標準差不同的正態分佈曲線。
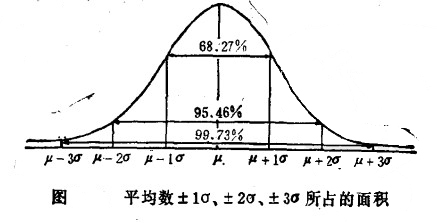
3.正態分佈曲線與橫軸間的總面積作為1，由平均數的兩側各距1個標準差的距離，與橫軸作兩條垂直線，兩條垂直線內的面積約占曲線內總面積的68.2796；從平均數的商測各距2個標準差的距離作兩條垂直線，則所占面積為95.46%，取3個標準差，則占99.73%，如圖所示。上述一定區間的面積占總面積的百分率，意味著總體的變數在此區間內分佈的概率。
上述一定區間變數的理論分佈概率，可以從實際調查的資料加以驗證。現以水稻雜交種“南優2號”100株株高的樣本資料，在\overline{X}土1s土2s、土3s三個範國內觀察值的分佈次數統計如表。
水稻雜交種“南優2號”100株株高的樣本資料，在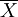
土1s土2s、土3s三個範國內觀察值的分佈次數
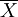| ±ks | 數值 | 範圍 | 範圍內觀察值次數 | 理論次數 |
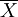| ±1s | 94.18±3.61 | 90.57-97.79 | 72 | 68.27 |
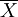| ±2s | 94.18±7.22 | 86.96-101.40 | 94 | 95.46 |
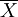| ±2s | 94.18±10.83 | 83.35-105.01 | 100 | 99.73 |
[編輯]
太差