正則形式的博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
正則形式的博弈（Normal form game）
目錄 |
在博弈論中，正則形式是描述博弈的一種方式。與延展形式不同，正則形式不用圖形來描述博弈，而是用矩陣來陳述博弈。與延展形式的表述方式相比，這種方式在識別出嚴格優勢策略和納什均衡上更有用，但會丟失某些信息。博弈的正則形式的表述方式包括如下部分：每個參與者所有顯然的和可能的策略，以及和與其相對應的收益。
在非完美信息的完全靜態博弈中，正則形式的表述方式詳細地說明瞭參與者策略空間和收益函數。策略空間是某個參與者的所有可能策略集合。策略是參與者在博弈的每個階段——不管在博弈中這個階段實際上是否會出現——將要採取的行動的完整計劃。每個參與者的收益函數，是從參與者策略空間的向量積到該參與者收益集合（一般是實數集，數字表示基數效用或序數效用——在正則形式的表述方式中常常是基數效用）的映射。也就是說，參與者的收益函數把策略組合（所有參與者策略的清單）作為它的輸入量，然後輸出參與者的收益。
| 合作 | 背叛 | |
|---|---|---|
| 合作 | 2, 2 | 0, 3 |
| 背叛 | 3, 0 | 1, 1 |
收益矩陣有助於剔除劣勢策略，而且經常被用於說明這個概念。例如，在囚徒困境中（右圖），參與者會發現因為其他人的背叛，合作成了嚴格劣勢策略。參與者會比較每列的第一個數字，在這個例子中，3>2且1>0。這表明無論橫排參與者怎樣選擇，豎排參與者選擇背叛都比較好些。類似地，參與者會比較每列的第二個數字，同樣也是3>2且1>0。這說明無論豎排參與者怎麼做，橫排參與者選擇背叛都比較好些。這就證明瞭此博弈唯一的納什均衡是（背叛，背叛）。
| 左，左 | 左，右 | 右，左 | 右，右 | |
|---|---|---|---|---|
| 頂 | 4, 3 | 4, 3 | -1, -1 | -1, -1 |
| 底 | 0, 0 | 3, 4 | 0, 0 | 3, 4 |
這些矩陣只表述同時（或者更一般地，信息不完美的）做出行動的博弈。上述矩陣不能表述甲先做出行動，被乙觀察到，然後乙再做出行動的博弈。因為在這個例子中，無法確定乙每次的策略。為了表述這種連續博弈，我們要列出乙在博弈進行期間所有的行動——儘管根據實際情況，某種行動決不會出現。和前面一樣，在這個博弈中乙有兩種選擇，左和右。與前面不一樣的是，視甲的行動不同而定，乙有四種策略。這些策略是：
1. 如果甲選擇頂，選擇左；否則，選擇左
2. 如果甲選擇頂，選擇左；否則，選擇右
3. 如果甲選擇頂，選擇右；否則，選擇左
4. 如果甲選擇定，選擇右；否則，選擇右
右圖是這個博弈的正則形式的表述方式。
為了用把博弈表述成正則形式，需要提供下列數據：
*表示參與者的有限集P，標記為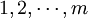
*每個參與者k在P里擁有有限個純策略.
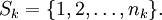
一個純策略組合是參與者策略的聯合，這是一個m元組.
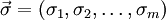
則有:
我們用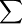
來表示策略組合的集合
收益函數形如
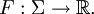
其預期解釋是博弈結束時給予單個參與者的獎品。相應地，為了完整地說明一個博弈，收益函數必須在參與者集 P= {1, 2, ..., m}中對每個參與者詳細說明。
定義：一個正則形式的博弈的結構形如
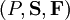
這裡 P = {1,2, ...,m}是參與者集合，
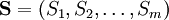
是純策略集合的一個m元組，每個純策略對應於一個參與者，而
是收益函數的m元組。
沒有理由在前面的討論中，把參與者數量有限或每個參與者的策略有限的博弈排除在外。因為要用到泛函分析的技巧，關於有限博弈的研究非常艱深。
| 乙選擇左 | 乙選擇右 | |
|---|---|---|
| 甲選擇頂 | 4, 3 | -1, -1 |
| 甲選擇底 | 0, 0 | 3, 4 |
有種博弈是參與者同時（或至少在做出行動前不觀察其他參與者的動作）做出行動，並按照上述已做出行動的組合獲得收益。右邊的矩陣是這種博弈得正則形式的表述方式。例如，如果甲做出行動“頂”，而乙做出行動“左”，則甲得到收收益4，乙得到收益3。在每個回合，第一個數字代表豎排參與者（此處為甲）的收益，第二個數字代表橫排參與者（此處為乙）的收益。
對稱博弈（其收益不是依賴於參與者選擇的動作）常常被表述為只有一種收益，即豎排參與者的收益。例如，左右兩邊的收益矩陣表述的是同一個博弈。
|
|
