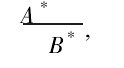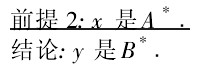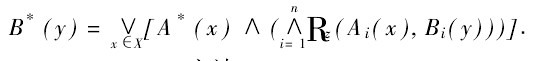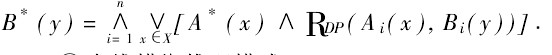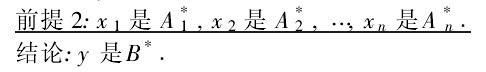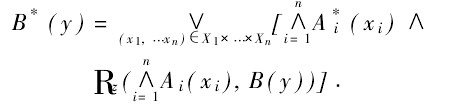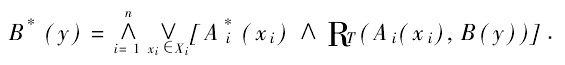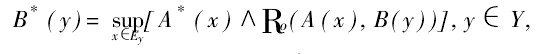模糊推理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　模糊推理作為近似推理的一個分支,是模糊控制的理論基礎。在實際應用中,它以數值計算而不是以符號推演為特征,它並不註重如像經典邏輯那樣的基於公理的形式推演或基於賦值的語義運算,而是通過模糊推理的演算法,由推理的前提計算出(而不是推演出)結論。1973年,Zadeh首先給出了模糊推理理論中最基本的推理規則即模糊分離規則FMP(fuzzy modus ponens)^[2],隨後被Zadeh和Mamdani等人演算法化^[3][4],形成了當今以推理合成規則CRI(compositional rule of inference)為主要基礎的各種模糊推理方法;但是王國俊近年認為模糊推理演算法以CRI為基礎存在缺陷,並提出了一種完全基於蘊涵運算元的3I演算法^[5]。30餘年來,模糊推理方法在工業生產控制、特別是在家電產品中的成功應用,使得它們在模糊系統以及自動控制等領域愈來愈受到人們的重視,如今在近似推理中已成為以數值計算而不是以符號推演為特征的一個研究發展方向。

　　然而,儘管這些基於Zadeh與Mamdani等人的工作而發展的各種模糊推理演算法用於經驗控制領域比其他方法有效,但從本質上不難看出實用中的模糊控制與邏輯控制的關聯越來越少,而對演算法的依賴卻越來越多^[6]。因此,用演算法代替模糊推理在理論上是否合理,其演算法的理論基礎是否可靠仍被人置疑,如Elkan在1994年國際人工智慧大會上所作的頗有影響的“模糊邏輯的似是而非的成功”的報告^[7]。

　　我們知道,在推理系統中,一個結論是由前提通過邏輯推理而得出的結果,但模糊推理演算法實質上是通過人為規定的方法計算出結果而不是推理出邏輯結論,具體就是將推理前提約定為一些運算元,再藉助於一些運算計算出結論,可見模糊推理演算法雖實用但主觀性強,本身的理論基礎貧弱。因此,將模糊推理演算法作為研究對象,從理論上對模糊推理演算法的構造基礎進行分析研究,論證用計算去替代模糊推理的演算法的理論依據是重要的。

　　1)模糊推理最基本的模式為模糊假言推理FMP(fuzzy modus ponens)^[8][9],其格式如下一般格式:。

　　前提1:若x是A,則y是B

　　模糊推理公式.jpg

　　形式化表示:

　　A→B

　　這裡,A,A ^* 是論域X上的模糊集,B,B ^* 是論域Y上的模糊集·1973年Zadeh提出著名的CRI(compositionalrule of inference)演算法·具體是,首先定義蘊涵運算元。

　　利用R_z把前提1中的A→B轉換為X×Y上一個模糊關係R(x,y):

　　然後,將前提2中A^*與R通過合成運算得到B^*,即

　　。

　　在模糊推理應用中,對於FMP,還有諸如Baldwin演算法、Mizumoto演算法等·但迄今為止,CRI演算法還是最基本、最重要的方法[4,6,10]·2)除了FMP外,模糊推理中還有多重(多條規則)模糊推理mcFMP(multiple conditional fuzzy modusponens)和多維模糊推理mdFMP(multidimensionalfuzzy modus ponens),其格式及典型演算法[6]如下(限於篇幅,分別隻列舉2種演算法):。

　　①多重模糊推理模式mcFMP

　　一般格式:

　　前提1:若x是A₁,則y是B₁,

　　　　　若x是A₂,則y是B₂,

　　　　　┇

　　　　　若x是A_n,則y是B_n

　　形式化格式

　　其中,A_i,A ^* 是論域X上的模糊集,B_i,B ^* 是論域Y上的模糊集,i=1,2,…,n,n≥2。

　　Zadeh演算法：

　　Dubois-Prade方法:

　　②多維模糊推理模式mdFMP

　　一般格式:

　　前提1:若x₁是A₁,x₂是是A_n,則。

　　y是B·

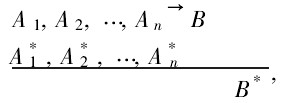
　　形式化格式:

　　其中,是論域X_i上的模糊集,B,B ^* 是論域Y上的模糊集,i=1,2,…,n。

　　Zadeh演算法:

　　Tsukamoto演算法:

　　R_T = R_z

　　從上述不難看出,對於多重模糊推理mcFMP以及多維模糊推理mdFMP,它們的演算法都是基於CRI的,所不同的是在演算法中採用了兩種途徑·第1種途徑是先把前提1中的n條規則聚合為一個模糊關係,然後再與前提2中的A ^* (或者進行合成(composition)求得B ^* ,如①,②中的Zadeh演算法;第2種途徑則是先將前提2中的A ^* (或)分別與前提1中的n條規則合成得到n個模糊關係,然後再進行合成求得B ^* ,如①中Dubois-Prade演算法和②中Tsukamoto演算法·30年來,雖然有不少學者提出過不同於CRI的模糊推理演算法,CRI演算法本身也有各種變形和發展,但實用中的大多數模糊推理演算法仍以CRI演算法的思想為基礎·然而,對於CRI演算法在將前提中的蘊涵關係轉化為模糊關係時使用了一次能體現推理思想的蘊涵運算元後,就直接藉助於合成運算給出推理結果,王國俊近年認為是一缺陷並提出了一種完全基於蘊涵運算元的3I演算法[4,10,13],即重新建立一個蘊涵運算元R_e,在3I原則(認為FMP應該是三重蘊涵關係下,提出R_e型3I演算法:

　　R_e(a,b),,當a≤b；否則,

　　其中

　　3I演算法雖然沒有在應用中檢驗,但它是一個不使用合成運算而採用三重模糊蘊涵關係的非CRI演算法,理論上具有一些良好特性,使得模糊推理演算法更具邏輯推理的特征。

　　從邏輯推理的本質來說,模糊邏輯與一般邏輯系統應具有相同的推理特征,既從一組前提出發推導出結論P的演繹是由邏輯系統的推理規則(公理也可作為推理規則)支配的,所不同的是,在模糊邏輯中前提和結論均允許是模糊命題。所謂模糊推理就是一種由具有模糊性的前提推導出結論的邏輯過程,因此,模糊推理由前提推導出模糊結論的準確程度,關鍵在於對前提1與前提2置以什麼樣的(模糊)關係結構,以及前提條件與結論又置以什麼樣的(模糊)關係結構。

　　對如上模糊推理演算法的思想以及構造進行分析,我們認為

　　1)演算法的基本思想就是把推理模式中用詞語描述的一組推理規則轉換成描述中變項之間的一種模糊關係,從而使模糊推理過程的實現都基於模糊關係。據此,可認為模糊推理演算法實質上是模糊推理的變換成的模糊關係的演算法。對具體演算法來說,無論是CRI演算法(以及以CRI為基礎的各種演算法)還是3I演算法,首先都遵循CRI演算法的第一步即利用蘊涵運算元,把已知前提1中的A→B轉化為X×Y上一個模糊關係R(x,y)。然後,Zadeh的思想是將FMP中所求的B*看做是以A→B和A ^* 為前提而推導的結論,即形式關係為A ^* ＆ ,這一點是符合一般邏輯的推理規則的;3I演算法的思想是將FMP中所求的B*看做是在以A→B為前提下由A ^* 推導出來的,即形式關係為。對於這兩種關於FMP推理意義的理解,若A ^* ＆為,則從邏輯語形的角度看,與是等同的,但是若從邏輯語義的角度看,前者比後者更符合FMP的推理涵義。然而,Zadeh在CRI演算法中卻將前提2與前提1之間的關係用複合運算刻畫,這一點是缺乏根據的,並且致使CRI演算法失去應有的推理涵義。相比之下,思想基於FMP的形式推理結構為的3I演算法,避免了CRI演算法的缺陷並具有許多良好性質·但是,在3I演算法中,結論B ^* (y)(B ^* 的隸屬度)的表達式從何而來,其中為什麼具有與CRI演算法相同的關係結構。

　　2)從演算法的結構看,模糊推理的各種演算法雖然各自採用的蘊涵運算元不同,但由於模糊蘊涵運算元是[0,1]×[0,1]到[0,1]上的映射,模糊蘊涵可由代表模糊“與”、模糊“或”、模糊“非”的3個基礎運算元t∧(t-模)、t∨(t-餘模)以及t^c(補)構造出來,並且,各種模糊推理演算法中求解B ^* (y)的表達式也以t-模、t-餘模和補t^c為基礎運算元,由此我們認為,除了針對mcFMP和mdFMP而提出的引進距離或貼近度等概念的演算法[4,10]外,諸如上述的模糊推理的各種經典演算法計算出的結論,實際上是由前提條件通過t∧,t∨和t^c三個基礎運算元在[0,1]上進行運算得出的結果,對模糊推理採用計算的演算法其本質上是對計算對象(推理前提)運用基礎運算元進行運算的方法,因此,通過這種方法計算得到的結果與計算對象之間就應存在某一數學關係。對此,我們得到如下結果。